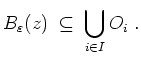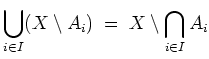- Es sei
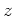 ein Berührpunkt von
ein Berührpunkt von
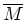 . Zu zeigen ist, daß
. Zu zeigen ist, daß
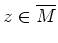 . Es sei
. Es sei
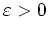 .
Dann gilt
d.h. es gibt ein
.
Dann gilt
d.h. es gibt ein
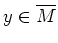 mit
mit
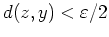 . Dann ist
. Dann ist
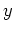 ein Berührpunkt von
ein Berührpunkt von
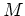 , d.h. es gilt
d.h. es gibt ein
, d.h. es gilt
d.h. es gibt ein
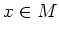 mit
mit
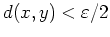 . Daraus folgt
d.h. es gilt
Also ist
. Daraus folgt
d.h. es gilt
Also ist
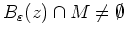 . Aus der Beliebigkeit von
. Aus der Beliebigkeit von
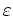 folgt, daß
folgt, daß
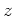 ein Berührpunkt von
ein Berührpunkt von
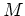 ist,
d.h. es gilt
ist,
d.h. es gilt
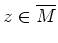 .
.
-
 :
:
- Es sei
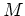 offen. Es sei
offen. Es sei
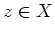 ein Berührpunkt von
ein Berührpunkt von
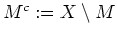 .
Zu zeigen ist, daß
.
Zu zeigen ist, daß
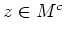 . Wir nehmen also an, daß
. Wir nehmen also an, daß
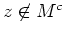 . Dann folgt
. Dann folgt
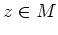 . Da
. Da
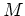 offen ist, gibt es ein
offen ist, gibt es ein
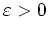 so, daß
so, daß
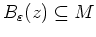 . Demnach ist
Dies widerspricht aber der Tatsache, daß
. Demnach ist
Dies widerspricht aber der Tatsache, daß
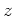 ein Berührpunkt von
ein Berührpunkt von
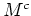 ist. Also war die Annahme falsch, und es gilt
ist. Also war die Annahme falsch, und es gilt
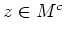 .
.
-
 :
:
- Es sei
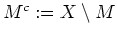 abgeschlossen. Es sei
abgeschlossen. Es sei
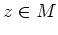 . Dann ist
. Dann ist
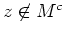 .
Da
.
Da
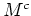 abeschlossen ist, ist
abeschlossen ist, ist
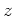 kein Berührpunkt von
kein Berührpunkt von
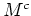 . Daher gibt es ein
. Daher gibt es ein
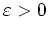 so, daß
Daraus folgt aber
so, daß
Daraus folgt aber
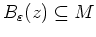 . Daher ist
. Daher ist
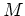 offen.
offen.
- Es sei
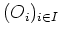 eine Familie offener Mengen in
eine Familie offener Mengen in
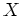 . Es sei
. Es sei
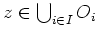 .
Dann gibt es ein
.
Dann gibt es ein
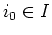 so, daß
so, daß
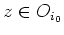 . Da
. Da
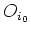 offen ist, gibt es ein
offen ist, gibt es ein
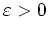 so, daß
so, daß
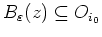 . Dann folgt aber auch
Demnach ist
. Dann folgt aber auch
Demnach ist
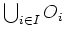 offen.
offen.
- Es seien
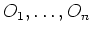 offene Mengen. Es sei
offene Mengen. Es sei
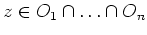 . Für jedes
. Für jedes
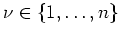 gilt
gilt
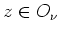 , und
, und
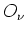 ist offen; also gibt es ein
ist offen; also gibt es ein
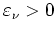 so, daß
Man setze nun
so, daß
Man setze nun
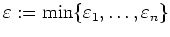 . Dann folgt
Also ist
. Dann folgt
Also ist
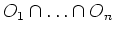 offen.
offen.
- Es sei
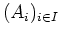 eine Familie abeschlossener Mengen in
eine Familie abeschlossener Mengen in
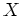 . Nach 1. ist dann
. Nach 1. ist dann
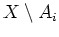 offen
für alle
offen
für alle
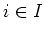 . Nach 2. und der Regel von de Morgan ist dann
offen. Nach 1. ist schließlich
. Nach 2. und der Regel von de Morgan ist dann
offen. Nach 1. ist schließlich
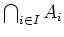 abgeschlossen.
abgeschlossen.
- Das folgt analog unter Verwendung von 1., 3. und der Regel von de Morgan.
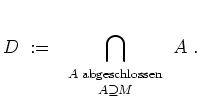
- Es sei
Nach 5. ist
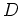 eine abgeschlossene Menge, und es gilt offenbar
eine abgeschlossene Menge, und es gilt offenbar
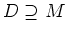 . Daraus folgt auch, daß
denn jeder Berührpunkt von
. Daraus folgt auch, daß
denn jeder Berührpunkt von
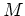 ist auch Berührpunkt von
ist auch Berührpunkt von
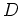 und liegt daher in
und liegt daher in
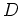 . Andererseits ist
. Andererseits ist
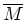 eine abgeschlossene Menge, und es gilt
eine abgeschlossene Menge, und es gilt
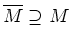 . Also nimmt
. Also nimmt
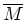 an der Durchschnittsbildung
in der Defintion von
an der Durchschnittsbildung
in der Defintion von
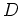 teil, und es folgt
Daraus folgt die Behauptung.
teil, und es folgt
Daraus folgt die Behauptung.
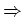 :
: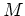 offen. Es sei
offen. Es sei
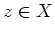 ein Berührpunkt von
ein Berührpunkt von
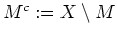 .
Zu zeigen ist, daß
.
Zu zeigen ist, daß
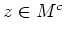 . Wir nehmen also an, daß
. Wir nehmen also an, daß
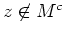 . Dann folgt
. Dann folgt
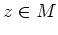 . Da
. Da
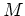 offen ist, gibt es ein
offen ist, gibt es ein
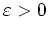 so, daß
so, daß
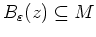 . Demnach ist
Dies widerspricht aber der Tatsache, daß
. Demnach ist
Dies widerspricht aber der Tatsache, daß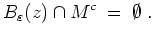
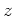 ein Berührpunkt von
ein Berührpunkt von
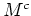 ist. Also war die Annahme falsch, und es gilt
ist. Also war die Annahme falsch, und es gilt
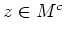 .
.
 :
: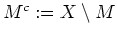 abgeschlossen. Es sei
abgeschlossen. Es sei
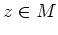 . Dann ist
. Dann ist
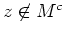 .
Da
.
Da
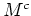 abeschlossen ist, ist
abeschlossen ist, ist
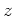 kein Berührpunkt von
kein Berührpunkt von
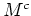 . Daher gibt es ein
. Daher gibt es ein
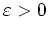 so, daß
Daraus folgt aber
so, daß
Daraus folgt aber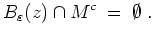
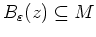 . Daher ist
. Daher ist
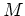 offen.
offen.