Potenzreihen, Exponentialfunktion und Logarithmus.

Potenzreihen.

Es sei $ \mbox{$z_0\in\mathbb{C}$}$ . Unter einer Potenzreihe um $ \mbox{$z_0$}$ verstehen wir eine unendliche Reihe der Form

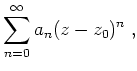
$ \mbox{$\displaystyle \sum_{n=0}^\infty a_n (z-z_0)^n\;, $}$
wobei $ \mbox{$(a_n)_{n\ge 0}$}$ eine Folge komplexer Zahlen sei, und $ \mbox{$z\in\mathbb{C}$}$ . Der Konvergenzradius dieser Potenzreihe ist definiert durch die Cauchy-Hadamardsche Formel
$ \mbox{$\displaystyle R \;:=\; \frac{1}{\varlimsup\limits_{n\to\infty}\sqrt[n]{\vert a_n\vert}}\;, $}$
wobei in dieser Definition $ \mbox{$\frac{1}{0}:=\infty$}$ und $ \mbox{$\frac{1}{\infty}:=0$}$ vereinbart sei.

Es gilt dann

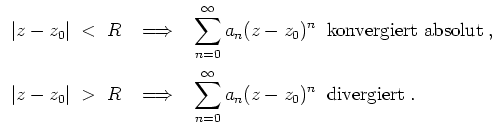
$ \mbox{$\displaystyle \begin{array}{rcl} \vert z-z_0\vert\;<\;R & \implies & \... ...playstyle\sum_{n=0}^\infty a_n (z-z_0)^n \;\;\text{divergiert}\;. \end{array}$}$
Die durch die Potenzreihe definierte Funktion
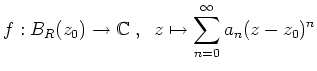
$ \mbox{$\displaystyle f: B_R(z_0)\to\mathbb{C}\;,\;\; z\mapsto \sum_{n=0}^\infty a_n (z-z_0)^n $}$
ist stetig.

Für $ \mbox{$\vert z-z_0\vert=R$}$ kann keine allgemeine Aussage über die Konvergenz getroffen werden. Zum Beispiel hat die Potenzreihe $ \mbox{$\sum_{n=1}^\infty\frac{z^n}{n}$}$ den Konvergenzradius $ \mbox{$1$}$ , und sie konvergiert für alle $ \mbox{$z\in\mathbb{C}$}$ mit $ \mbox{$\vert z\vert\le 1$}$ und $ \mbox{$z\ne 1$}$ .

Alternativ zur Cauchy-Hadamardschen Formel kann der Konvergenzradius im Falle der Existenz des folgenden Grenzwertes auch durch die Formel

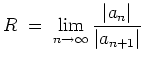
$ \mbox{$\displaystyle R \;=\; \lim_{n\to\infty}\frac{\vert a_n\vert}{\vert a_{n+1}\vert} $}$
berechnet werden.

Exponentialfunktion.

Die Exponentialfunktion ist definiert durch

$ \mbox{$\displaystyle \exp:\mathbb{C}\to\mathbb{C}\;,\;\; z\mapsto \exp(z)\;:=\;e^z\;:=\;\sum_{n=0}^\infty\frac{z^n}{n!}\;. $}$
Der Konvergenzradius dieser Potenzreihe ist $ \mbox{$R=\infty$}$ , d.h. sie konvergiert für alle $ \mbox{$z\in\mathbb{C}$}$ , und sie stellt eine stetige Funktion dar.

Die Exponentialfunktion erfüllt die Funktionalgleichung

$ \mbox{$\displaystyle e^{a+b} \;=\; e^a\cdot e^b $}$
für alle $ \mbox{$a,b\in\mathbb{C}$}$ .

Die Sinus- und Cosinusfunktion sind definiert durch

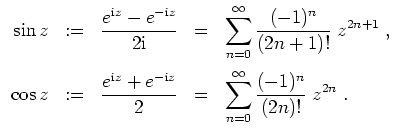
$ \mbox{$\displaystyle \begin{array}{rclcl} \sin z &:=& \dfrac{e^{\text{i}z}-e^... ...=& \displaystyle\sum_{n=0}^\infty \frac{(-1)^n}{(2n)!}\;z^{2n}\;. \end{array}$}$
für alle $ \mbox{$z\in\mathbb{C}$}$ . Es gilt die Eulersche Gleichung
$ \mbox{$\displaystyle e^{\text{i}z} \;=\; \cos z + \text{i}\sin z\;. $}$

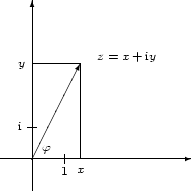
Argument.

Zu jeder komplexen Zahl $ \mbox{$z\ne 0$}$ gibt es ein eindeutig bestimmtes $ \mbox{$\varphi\in(-\pi,\pi]$}$ so, daß

$ \mbox{$\displaystyle z \;=\; \vert z\vert\cdot e^{\text{i}\varphi}\;. $}$
Die Zahl $ \mbox{$\varphi$}$ heißt das Argument von $ \mbox{$z$}$ , in Zeichen $ \mbox{$\varphi=\text{Arg }z$}$ .

Dies entspricht der Polarkoordinatendarstellung von $ \mbox{$z=x+\text{i}y$}$ , aufgefaßt als Element $ \mbox{$(x,y)\in\mathbb{R}^2$}$ , in der Form

$ \mbox{$\displaystyle (x,y) \;=\; r\cdot (\cos\varphi\;,\;\sin\varphi)\;, $}$
wobei $ \mbox{$r:=\vert z\vert=\sqrt{x^2+y^2}$}$ . Das Argument ist gerade der Winkel, den der Vektor $ \mbox{$(x,y)$}$ mit der reellen Achse einschließt.


\begin{picture}(100,120) \put( -20, 20){\vector(1,0){120}} \put( 20, 17){\line(0... ...t( 41, 82){{$\mbox{$\scriptstyle z \; =\; x \, + \,\text{i} y$}$}} \end{picture}

Die Funktion $ \mbox{$\text{Arg}:\mathbb{C}\setminus\{0\}\to(-\pi,\pi]$}$ ist stetig auf der geschlitzten Ebene

$ \mbox{$\displaystyle \mathbb{C}_- \;:=\; \mathbb{C}\setminus\mathbb{R}_{\le 0}\;. $}$
\includegraphics[width=6cm]{geschlitzt.eps}

Logarithmus.

Für $ \mbox{$z\in\mathbb{C}\setminus\{0\}$}$ definieren wir den Logarithmus von $ \mbox{$z$}$ durch

$ \mbox{$\displaystyle \text{Log } z \;:=\; \log\vert z\vert+\text{i}\;\text{Arg }z\;. $}$
Dies ist gerade die Umkehrfunktion der bijektiven Abbildung
$ \mbox{$\displaystyle \exp:\{z\in\mathbb{C}\;\vert\; -\pi<\text{Im }z\le\pi\} \;\to\; \mathbb{C}\setminus\{0\}\;, $}$
welche den Horizontalstreifen $ \mbox{$\{z\in\mathbb{C}\;\vert\; -\pi<\text{Im }z\le\pi\}$}$ bijektiv auf die punktierte Ebene $ \mbox{$\mathbb{C}\setminus\{0\}$}$ abbildet. Es gilt
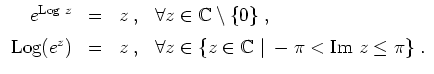
$ \mbox{$\displaystyle \begin{array}{rcll} e^{\text{Log } z} &=& z\;, & \forall... ...\forall z\in\{z\in\mathbb{C}\;\vert\; -\pi<\text{Im }z\le\pi\}\;. \end{array}$}$
Der Logarithmus ist stetig auf der geschlitzten Ebene $ \mbox{$\mathbb{C}_-$}$ .

Der Logarithmus läßt sich als eine Potenzreihe um den Punkt $ \mbox{$1$}$ darstellen vermöge

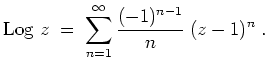
$ \mbox{$\displaystyle \text{Log }z \;=\; \sum_{n=1}^\infty \frac{(-1)^{n-1}}{n}\;(z-1)^n\;. $}$
Diese Potenzreihe hat den Konvergenzradius $ \mbox{$1$}$ . Die Identität gilt für alle $ \mbox{$z\in\mathbb{C}$}$ mit $ \mbox{$\vert z-1\vert\le 1$}$ und $ \mbox{$z\ne 0$}$ .

Die allgemeine Potenz ist definiert durch

$ \mbox{$\displaystyle a^b \;:=\; e^{b\;\text{Log } a} $}$
für alle $ \mbox{$a\in\mathbb{C}\setminus\{0\}$}$ .