![$ \mbox{$\displaystyle
R\;=\;\displaystyle{ \left(\varlimsup_{k \to \infty}{\sqrt[k]{1/5^k}}\right)^{-1}}\;=\; \frac{1}{1/5} \;=\; 5
$}$](img2.png)
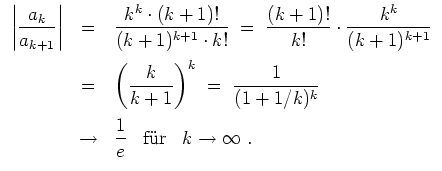
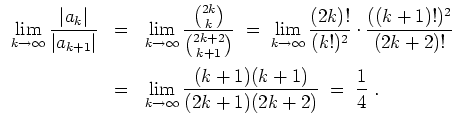
Daher konvergiert die Reihe
![]() für
für
![]() , i.e. für
, i.e. für
![]() ,
und sie divergiert für
,
und sie divergiert für
![]() , i.e. für
, i.e. für
![]() .
.
Die Reihe
![]() besitzt also den Konvergenzradius
besitzt also den Konvergenzradius
![]() .
.
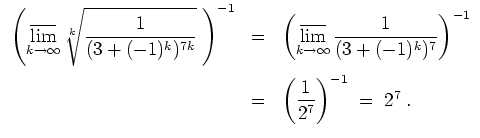
- Fall 1:
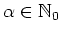 .
Dann gilt
.
Dann gilt
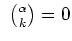 für alle
für alle
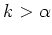 . Der Konvergenzradius ist in diesem Fall also
. Der Konvergenzradius ist in diesem Fall also
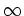 .
.
- Fall 2:
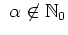 . Dann folgt
Der Konvergenzradius ist in diesem Fall also
. Dann folgt
Der Konvergenzradius ist in diesem Fall also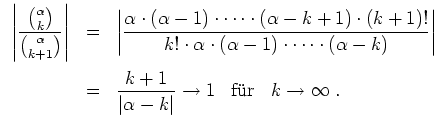
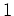 .
.