- Es sei
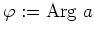 und
und
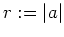 . Dann gilt
Wir setzen
. Dann gilt
Wir setzen
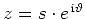 an und berechnen
Also gilt
Es gibt also genau
an und berechnen
Also gilt
Es gibt also genau
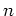 verschiedene Lösungen der Gleichung
verschiedene Lösungen der Gleichung
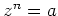 , und diese sind gegeben durch
, und diese sind gegeben durch
- Es gilt
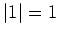 und
und
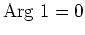 . Nach 1. gibt es also genau acht Lösungen der Gleichung
. Nach 1. gibt es also genau acht Lösungen der Gleichung
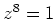 , nämlich
Setzt man diese acht Werte für
, nämlich
Setzt man diese acht Werte für
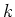 ein, so vereinfachen sich die Lösungen zu
Es handelt sich also um die Ecken des regelmäßigen Achtecks.
ein, so vereinfachen sich die Lösungen zu
Es handelt sich also um die Ecken des regelmäßigen Achtecks.
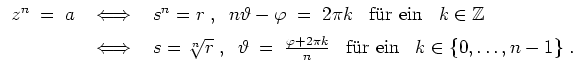
![\includegraphics[width=5cm]{achteck.eps}](img16.png)
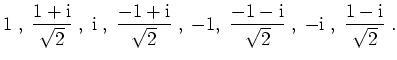
![\includegraphics[width=5cm]{achteck.eps}](img16.png)