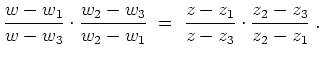Stereographische Projektion.
Wir identifizieren die komplexe Zahlenebene
![]() mit der
mit der
![]() -Ebene im dreidimensionalen Raum
-Ebene im dreidimensionalen Raum
![]() .
Es sei
.
Es sei
![]() die Einheitssphäre im
die Einheitssphäre im
![]() , d.h.
, d.h.
![\includegraphics[width=10cm]{spherical.eps}](img9.png)
Es sei
![]() die stereographische Projektion von
die stereographische Projektion von
![]() . Löst man die Gleichungen der Geraden und der Sphäre
auf, so ergeben sich die Formeln
. Löst man die Gleichungen der Geraden und der Sphäre
auf, so ergeben sich die Formeln
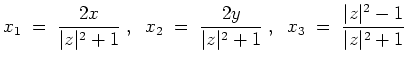
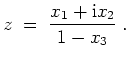
Der fehlende Punkt
![]() werde zusätzlich mit einem Punkt
werde zusätzlich mit einem Punkt
![]() identifiziert, d.h.
wir setzen
identifiziert, d.h.
wir setzen
![]() . So erhalten wir eine bijektive Abbildung
. So erhalten wir eine bijektive Abbildung
Chordale Metrik.
Auf der Riemannschen Zahlenkugel ist die euklidische Metrik des
![]() gegeben, d.h.
für
gegeben, d.h.
für
![]() ,
,
![]() gilt
gilt
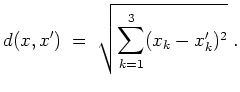
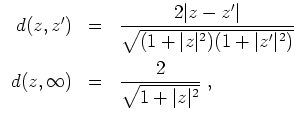
Wegen der Stetigkeit von
![]() und ihrer Umkehrabbildung ist die chordale Metrik auf
und ihrer Umkehrabbildung ist die chordale Metrik auf
![]() äquivalent zur gewöhnlichen euklidischen Metrik, d.h. alle topologischen Begriffe stimmen unter beiden Metriken überein.
äquivalent zur gewöhnlichen euklidischen Metrik, d.h. alle topologischen Begriffe stimmen unter beiden Metriken überein.
Auf diese Weise haben wir
![]() zu einem kompakten metrischen Raum gemacht.
zu einem kompakten metrischen Raum gemacht.
Die
![]() -Umgebungen des Punktes
-Umgebungen des Punktes
![]() bezüglich der chordalen Metrik sind gerade die Mengen der Form
bezüglich der chordalen Metrik sind gerade die Mengen der Form
Möbiustransformationen.
Eine gebrochen lineare Abbildung ist eine Abbildung der Form
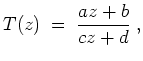
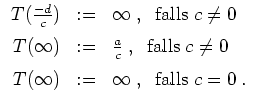
Die Matrix
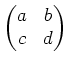 ist durch die Möbiustransformation
ist durch die Möbiustransformation
![]() nur bis auf eine
multiplikative Konstante in
nur bis auf eine
multiplikative Konstante in
![]() bestimmt.
bestimmt.
Die Verkettung zweier Möbiustransformationen
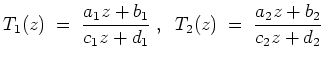
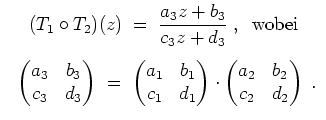
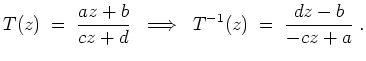
Jede Möbiustransformation bildet somit
![]() bijektiv auf sich selbst ab.
bijektiv auf sich selbst ab.
Abbildungsverhalten von Möbiustransforamtionen.
Unter einem verallgemeinerten Kreis in
![]() versteht man eine Gerade zusammen mit dem Punkt
versteht man eine Gerade zusammen mit dem Punkt
![]() oder
einen Kreis in
oder
einen Kreis in
![]() . Dieser Begriff ist gerechtfertigt, denn unter der stereographischen Projektion entsprechen
verallgemeinerte Kreise in
. Dieser Begriff ist gerechtfertigt, denn unter der stereographischen Projektion entsprechen
verallgemeinerte Kreise in
![]() eineindeutig den Kreisen auf der Riemannschen Zahlenkugel.
eineindeutig den Kreisen auf der Riemannschen Zahlenkugel.
Eine Orientierung eines verallgemeinerten Kreises
![]() ist ein Tripel
ist ein Tripel
![]() von Punkten auf
von Punkten auf
![]() . Eine Orientierung ist anschaulich als Durchlaufsinn oder Durchlaufrichtung zu verstehen. Zu einem verallgemeinerten Kreis
. Eine Orientierung ist anschaulich als Durchlaufsinn oder Durchlaufrichtung zu verstehen. Zu einem verallgemeinerten Kreis
![]() mit
Orientierung kann man stets das links von
mit
Orientierung kann man stets das links von
![]() liegende Gebiet
liegende Gebiet
![]() definieren. Ist
definieren. Ist
![]() ein Kreis, so ist
ein Kreis, so ist
![]() das Innere oder
das Äußere von
das Innere oder
das Äußere von
![]() , je nachdem ob die gewählte Orientierung mathematisch positiv oder negativ ist. Ist
, je nachdem ob die gewählte Orientierung mathematisch positiv oder negativ ist. Ist
![]() eine Gerade,
so ist
eine Gerade,
so ist
![]() eine Halbebene.
eine Halbebene.
Eine Möbiustransformation bildet verallgemeinerte Kreise auf verallgemeinerte Kreise ab, und erhält dabei die Orientierung
und das links liegende Gebiet. Ist also
![]() eine Möbiustransformation,
eine Möbiustransformation,
![]() ein verallgemeinerter Kreis mit Orientierung
ein verallgemeinerter Kreis mit Orientierung
![]() und
und
![]() das links von
das links von
![]() liegende Gebiet, so ist
liegende Gebiet, so ist
![]() ein verallgemeinerter Kreis mit Orientierung
ein verallgemeinerter Kreis mit Orientierung
![]() , und
, und
![]() ist das links von
ist das links von
![]() liegende Gebiet.
liegende Gebiet.
Konstruktion von Möbsiutransformationen.
Es seien
![]() bzw.
bzw.
![]() jeweils paarweise verschieden.
Dann gibt es genau eine Möbiustransformation, welche
jeweils paarweise verschieden.
Dann gibt es genau eine Möbiustransformation, welche
![]() auf
auf
![]() abbildet für
abbildet für
![]() . Diese kann durch die
Sechs-Punkte-Formel berechnet werden. Man schreibe
. Diese kann durch die
Sechs-Punkte-Formel berechnet werden. Man schreibe