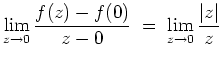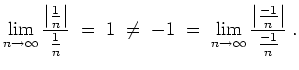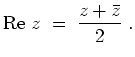
Alternativ zeige man, daß die Cauchy-Riemannschen Differentialgleichungen in keinem Punkt gelten.
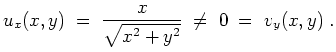
Im Punkt
![]() existiert der Grenzwert
existiert der Grenzwert
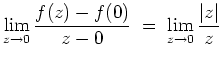
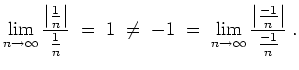
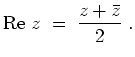
Alternativ zeige man, daß die Cauchy-Riemannschen Differentialgleichungen in keinem Punkt gelten.
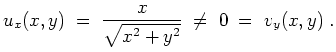
Im Punkt
![]() existiert der Grenzwert
existiert der Grenzwert