Lösung.

Da $ \mbox{$f$}$ komplex differenzierbar in $ \mbox{$z_0$}$ ist, gibt es eine lineare Approximation

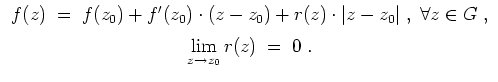
$ \mbox{$\displaystyle \begin{array}{c} f(z)\;=\; f(z_0) + f'(z_0)\cdot (z-z_... ...space*{2mm}\\ \displaystyle\lim_{z \to z_0} r(z) \;=\; 0\;. \end{array} $}$
Daraus folgt sofort
$ \mbox{$\displaystyle \lim_{z \to z_0} f(z) \;=\; f(z_0)\;, $}$
d.h. $ \mbox{$f$}$ ist stetig in $ \mbox{$z_0$}$ .

Alternativ, faßt man $ \mbox{$f$}$ als zweidimensionales Vektorfeld zweier reeller Veränderlicher auf, so folgt die Stetigkeit aus der totalen Differenzierbarkeit, wie aus der reellen mehrdimensionalen Analysis bekannt.