Holomorphie.

Komplexe Differenzierbarkeit.

Es sei $ \mbox{$G \subseteq \mathbb{C}$}$ eine offene Menge. Eine Funktion $ \mbox{$f: G \to \mathbb{C}$}$ heißt komplex differenzierbar in $ \mbox{$\ z_0 \in G$}$ , falls der Grenzwert

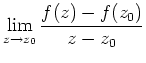
$ \mbox{$\displaystyle \lim_{z \to z_0} \frac{ f(z)-f(z_0)}{z-z_0} $}$
existiert. In diesem Falle heißt dieser Grenzwert die Ableitung von $ \mbox{$f$}$ in $ \mbox{$z_0$}$ und wird mit $ \mbox{$f'(z_0)$}$ bezeichnet.

Anschaulich bedeutet Differenzierbarkeit in einem Punkt $ \mbox{$z_0$}$ , daß sich die Funktion in der Nähe von $ \mbox{$z_0$}$ gut linear approximieren läßt. Genauer, die Funktion $ \mbox{$f$}$ ist differenzierbar in $ \mbox{$\ z_0 \in G$}$ genau dann, wenn es eine Konstante $ \mbox{$c \in \mathbb{C}$}$ und eine Funktion $ \mbox{$r: G \to \mathbb{C} $}$ gibt derart, daß

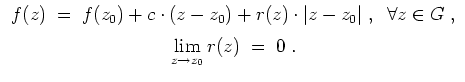
$ \mbox{$\displaystyle \begin {array}{c} f(z)\;=\; f(z_0)+ c\cdot (z-z_0) + r(z... ..., \vspace{2mm}\\ \displaystyle\lim_{z \to z_0} r(z) \;=\; 0 \;. \end{array}$}$
Es gilt dann $ \mbox{$c= f'(z_0)$}$ .

Ist $ \mbox{$f$}$ in jedem Punkt des Definitionsbereiches $ \mbox{$G$}$ komplex differenzierbar, so heißt $ \mbox{$f$}$ holomorph oder auch analytisch.

Ist $ \mbox{$f:\mathbb{C}\to\mathbb{C}$}$ auf der gesamten komplexen Ebene holomorph, so heißt $ \mbox{$f$}$ eine ganze Funktion.

Differenzierbarkeitsregeln.

Es seien $ \mbox{$f,g:G \to \mathbb{C} $}$ komplex differenzierbar in $ \mbox{$\ z_0 \in G$}$ und $ \mbox{$\lambda, \mu \in \mathbb{C}$}$ . Dann sind auch die Funktionen $ \mbox{$\lambda f + \mu g $}$ , $ \mbox{$\ f\cdot g$}$ und $ \mbox{$\ \frac {f}{g}$}$ komplex differenzierbar in $ \mbox{$z_0$}$ , und es gelten die folgenden Regeln.

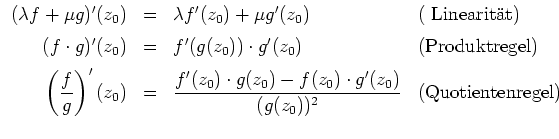
$ \mbox{$\displaystyle \begin {array}{rcll} (\lambda f + \mu g )'(z_0) &=& \lam... ...g'(z_0)}{(g(z_0))^2} & \text {(Quotientenregel)} \vspace{2mm}\\ \end{array}$}$
Für die Betrachtung des Quotienten $ \mbox{$\ \frac {f}{g}$}$ sei dabei zusätzlich $ \mbox{$g(z_0) \ne 0$}$ vorausgesetzt.

Es seien $ \mbox{$f: G \to \mathbb{C}$}$ komplex differenzierbar in $ \mbox{$\ z_0 \in G$}$ und $ \mbox{$f(G) \subseteq H $}$ mit einer offenen Menge $ \mbox{$H \subseteq \mathbb{C} $}$ . Es sei ferner $ \mbox{$g: H \to \mathbb{C}$}$ komplex differenzierbar in $ \mbox{$f(z_0)$}$ . Dann ist $ \mbox{$g \circ f$}$ komplex differenzierbar in $ \mbox{$z_0$}$ , und es gilt

$ \mbox{$\displaystyle (g \circ f)'(z_0) \;=\; g'(f(z_0)) \cdot f'(z_0) \;\;\;\; \text {(Kettenregel)}. $}$

Es sei nun $ \mbox{$f: G \to H$}$ holomorph und bijektiv, wobei $ \mbox{$G,H \subseteq \mathbb{C}$}$ offene Mengen seien. Es sei außerdem $ \mbox{$f'(z) \ne 0$}$ für alle $ \mbox{$z \in G$}$ . Dann ist auch die Umkehrfunktion $ \mbox{$\ f^{-1} : H \to G $}$ holomorph, und es gilt

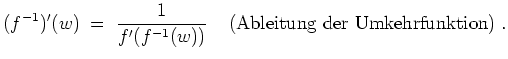
$ \mbox{$\displaystyle (f^{-1})'(w)\;=\; \frac{1}{f'(f^{-1}(w))} \;\;\;\; \text{(Ableitung der Umkehrfunktion)}\;. $}$

Cauchy-Riemannsche Differentialgleichungen.

Wir wollen einen Zusammenhang zwischen komplexer und totaler Differenzierbarkeit herstellen.

Es seien $ \mbox{$G \subseteq \mathbb{C}$}$ , $ \mbox{$f: G \to \mathbb{C}$}$ eine Funktion und $ \mbox{$z_0=x_0+\text{i}\,y_0\in G$}$ ein innerer Punkt. Wir setzen

$ \mbox{$\displaystyle u(x,y)\;:=\; \text{Re }f(x+\text{i}y)\;,\;\; v(x,y)\;:=\; \text{Im }f(x+\text{i}\,y)\;, $}$
aufgefaßt als Funktionen zweier reeller Veränderlicher. Dann sind die beiden folgenden Aussagen äquivalent.
(i)
$ \mbox{$f$}$ ist in $ \mbox{$z_0$}$ komplex differenzierbar.
(ii)
Das Vektorfeld $ \mbox{$(u,v)^\text{t}$}$ ist in $ \mbox{$(x_0,y_0)$}$ total differenzierbar, und es gelten die Cauchy-Riemannschen Differentialgleichungen im Punkt $ \mbox{$(x_0,y_0)$}$
$ \mbox{$\displaystyle u_x(x_0,y_0)\;=\; v_y(x_0,y_0)\;,\;\;u_y(x_0,y_0)\;=\; -v_x(x_0,y_0)\;. $}$
Es gilt dann
$ \mbox{$\displaystyle f'(z_0)\;=\; u_x(x_0,y_0) + \text{i}\,v_x(x_0,y_0) \;=\; v_y(x_0,y_0) - \text{i}\,u_y(x_0,y_0)\;. $}$

Mittelwertungleichung.

Es sei $ \mbox{$G \subseteq \mathbb{C}$}$ eine offene Menge und $ \mbox{$f: G \to \mathbb{C}$}$ sei holomorph. Es seien $ \mbox{$z,z_0\in G$}$ derart, daß die Verbindungsstrecke $ \mbox{$[z,z_0]$}$ in $ \mbox{$G$}$ enthalten ist, d.h.

$ \mbox{$\displaystyle [z,z_0] \;:=\; \{(1-\lambda)z+\lambda z_0\;\vert\; \lambda\in[0,1]\}\;\subseteq\; G\;. $}$
Dann gilt die Mittelwertungleichung
$ \mbox{$\displaystyle \vert f(z)-f(z_0)\vert \;\le\; \sup\{\vert f'(\xi)\vert\;\vert\; \xi\in[z,z_0]\}\cdot\vert z-z_0\vert\;. $}$
Vorsicht: Ein Analogon zum Mittelwertsatz der reellen Analysis für skalare Funktionen gilt für komplexwertige Funktionen i.a. nicht.

Holomorphie von Potenzreihen.

Es sei eine Potenzreihe $ \mbox{$\sum_{n=0}^\infty a_n(z-z_0)^n$}$ gegeben, wobei $ \mbox{$z_0,a_n\in\mathbb{C}$}$ , und es sei $ \mbox{$R$}$ der Konvergenzradius der Potenzreihe. Es sei

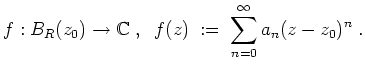
$ \mbox{$\displaystyle f:B_R(z_0)\to\mathbb{C}\;,\;\; f(z) \;:=\; \sum_{n=0}^\infty a_n(z-z_0)^n\;. $}$
Dann ist $ \mbox{$f$}$ holomorph. (Im Falle $ \mbox{$R=\infty$}$ sei $ \mbox{$B_R(z_0):=\mathbb{C}$}$ .) Es gilt dann
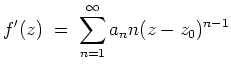
$ \mbox{$\displaystyle f'(z) \;=\; \sum_{n=1}^\infty a_n n (z-z_0)^{n-1} $}$
für alle $ \mbox{$z\in B_R(z_0)$}$ , und die letztgenannte Potenzreihe hat denselben Konvergenzradius $ \mbox{$R$}$ .

Kurz: Eine Potenzreihe ist holomorph im Inneren des Konvergenzbereiches, und die Ableitung ergibt sich durch Ableitung der Summanden.

Speziell ist die Exponentialfunktion holomorph, und es gilt $ \mbox{$\exp' =\exp$}$ .