Lösung.

  1. Es wird
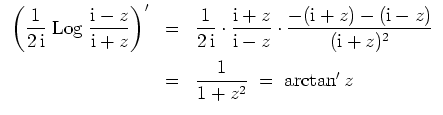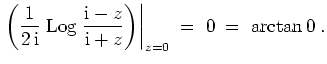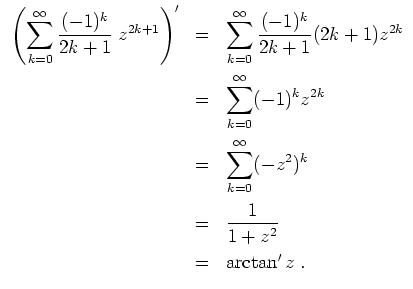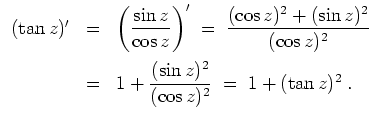
    $ \mbox{$\displaystyle \begin{array}{rcl} (\tan z)' &=& \left(\dfrac{\sin z... ... &=& 1+\dfrac{(\sin z)^2}{(\cos z)^2} \;=\; 1+(\tan z)^2\;. \end{array} $}$
  2. Es wird
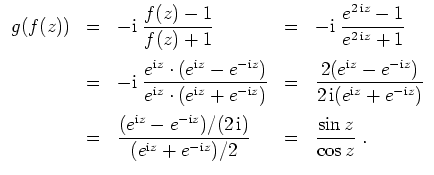
    $ \mbox{$\displaystyle \begin{array}{rclcl} g(f(z)) &=& -\text{i} \;\dfrac{... ...^{\text{i}z}+e^{-\text{i}z})/2} &=& \dfrac{\sin z}{\cos z}\;. \end{array} $}$
  3. (i)
    Zunächst ist die Abbildung
    $ \mbox{$\displaystyle \begin{array}{rcl} G \;=\; \left\{z\in\mathbb{C}\;\ver... ...m }z\vert<\pi\}\vspace*{2mm}\\ z &\longmapsto& 2\,\text{i}z \end{array} $}$
    bijektiv.
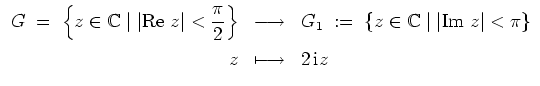
    (ii)
    Wir beachten, daß die Abbildung
    $ \mbox{$\displaystyle G_1\to\mathbb{C}_-\;,\;\; z\mapsto e^z $}$
    bijektiv ist.
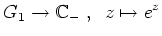
    (iii)
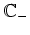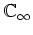    Wir zeigen nun noch, daß $ \mbox{$g$}$ die geschlitzte Ebene $ \mbox{$\mathbb{C}_-$}$ bijektiv auf $ \mbox{$H$}$ abbildet. Die Abbildung $ \mbox{$g$}$ ist eine Möbiustransformation, d.h. sie bildet $ \mbox{$\mathbb{C}_\infty$}$ bijektiv nach 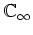$ \mbox{$\mathbb{C}_\infty$}$ ab. Ferner gilt
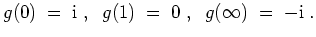
    $ \mbox{$\displaystyle g(0) \;=\; \text{i}\;,\;\; g(1) \;=\; 0\;,\;\; g(\infty) \;=\; -\text{i}\;. $}$
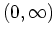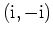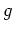    Also wird die nach rechts orientierte reelle Achse auf die nach unten orientierte imaginäre Achse abgebildet, und das Intervall $ \mbox{$(0,\infty)$}$ wird dabei auf das Intervall $ \mbox{$(\text{i},-\text{i})$}$ abgebildet. Daraus folgt, daß $ \mbox{$g$}$ die geschlitzte Ebene 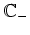$ \mbox{$\mathbb{C}_-$}$ bijektiv auf 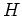$ \mbox{$H$}$ abbildet.
    Aus (i), (ii) und (iii) sowie 2. folgt die Behauptung.

  4. Nach 3. ist $ \mbox{$\tan:G\to H$}$ bijektiv und holomorph. Ferner ist nach 1.
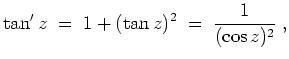
    $ \mbox{$\displaystyle \tan' z \;=\; 1+(\tan z)^2 \;=\; \dfrac{1}{(\cos z)^2}\;, $}$
    d.h. es gilt $ \mbox{$\tan' z\ne 0$}$ für alle $ \mbox{$z\in G$}$ . Daher besitzt die Tangensfunktion eine holomorphe Umkehrfunktion $ \mbox{$\arctan$}$ , und nach der Formel für die Ableitung der Umkehrfunktion ergibt sich
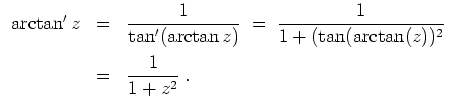
    $ \mbox{$\displaystyle \begin{array}{rcl} \arctan' z &=& \dfrac{1}{\tan'(\a... ...(\tan(\arctan(z))^2}\vspace*{2mm}\\ &=& \dfrac{1}{1+z^2}\;. \end{array} $}$

  5. Es gilt
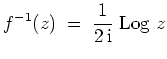
    $ \mbox{$\displaystyle f^{-1}(z) \;=\; \dfrac{1}{2\,\text{i}}\;\text{Log }z $}$
    für alle $ \mbox{$z\in \mathbb{C}_-$}$ , und nach der bekannten Formel für die Umkehrabbildung einer Möbiustransformation gilt
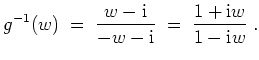
    $ \mbox{$\displaystyle g^{-1}(w) \;=\; \dfrac{w-\text{i}}{-w-\text{i}}\;=\; \dfrac{1+\text{i}w}{1-\text{i}w}\;. $}$
    Wegen $ \mbox{$\tan=g\circ f$}$ ist
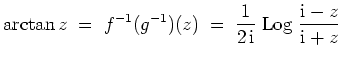
    $ \mbox{$\displaystyle \arctan z \;=\; f^{-1}(g^{-1})(z)\;=\; \dfrac{1}{2\,\text{i}}\;\textrm{Log }\dfrac{\text{i}-z}{\text{i}+z} $}$
    für alle $ \mbox{$z\in H$}$ .

    Alternativ kann man unter Verwendung von 3. die Ableitungen der beiden Funktionen vergleichen und die Gleicheit der Funktionen in einem Punkt überprüfen. Es gilt nämlich

    $ \mbox{$\displaystyle \begin{array}{rcl} \left( \dfrac{1}{2\,\text{i}}\;\tex... ...+z)^2}\vspace*{2mm}\\ &=& \dfrac{1}{1+z^2} \;=\; \arctan'z \end{array} $}$
    und
    $ \mbox{$\displaystyle \left.\left( \dfrac{1}{2\,\text{i}}\;\textrm{Log }\dfrac{\text{i}-z}{\text{i}+z}\right)\right\vert _{z=0}\;=\;0\;=\;\arctan 0 \;. $}$

  6. Wir überprüfen , ob die Ableitungen beider Seiten übereinstimmen , und ob die behauptete Gleichheit in einem Punkt gilt. Es wird
    $ \mbox{$\displaystyle \begin{array}{rcl} \left(\displaystyle\sum_{k=0}^{\inf... ...}\\ &=& \dfrac{1}{1+z^2} \vspace{2mm}\\ &=& \arctan'z\;. \end{array} $}$
    Außerdem gilt
    $ \mbox{$\displaystyle \arctan 0\;=\;0\;=\; \sum_{k=0}^{\infty} 0 \;. $}$
    Es folgt also die Behauptung.