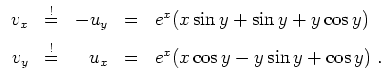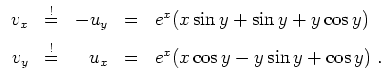Gemäß den Cauchy-Riemannschen Differentialgleichungen muß gelten
Integration von
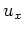 nach
nach
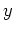 liefert den Ansatz
mit einer differenzierbaren Funktion
liefert den Ansatz
mit einer differenzierbaren Funktion
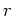 . Die Berechnung von
. Die Berechnung von
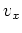 und der Vergleich mit
und der Vergleich mit
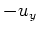 zeigen, daß man
zeigen, daß man
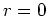 wählen kann.
Da
wählen kann.
Da
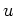 und
und
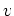 total differenzierbar sind und nach Konstruktion die Cauchy-Riemannschen Differentialgleichungen erfüllen,
ist
total differenzierbar sind und nach Konstruktion die Cauchy-Riemannschen Differentialgleichungen erfüllen,
ist
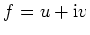 holomorph.
holomorph.