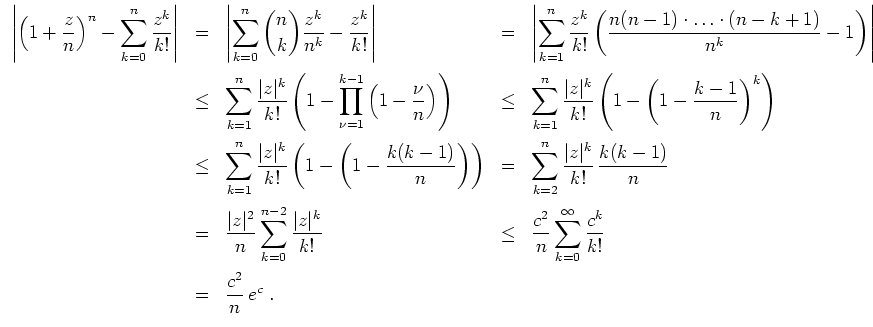Lösung.

Es sei 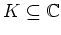$ \mbox{$K\subseteq\mathbb{C}$}$ eine kompakte Teilmenge. Wir wollen zeigen, daß 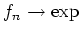$ \mbox{$f_n\to\exp$}$ gleichmäßig auf 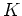$ \mbox{$K$}$ . Es sei

$ \mbox{$\displaystyle c \;:=\; \max\{\vert z\vert\;:\; z\in K\}\;. $}$

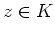
Es gilt für alle $ \mbox{$z\in K$}$

$ \mbox{$\displaystyle \begin{array}{rclcl} \left\vert\left(1+\dfrac{z}{n}\righ... ...\infty\frac{c^k}{k!}\vspace*{2mm}\\ &=& \dfrac{c^2}{n}\, e^c\;. \end{array}$}$
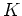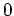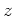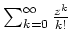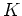Der letzte Term konvergiert auf $ \mbox{$K$}$ gleichmäßig gegen $ \mbox{$0$}$ , da er von $ \mbox{$z$}$ unabhängig ist. Da außerdem die Reihe $ \mbox{$\sum_{k=0}^\infty\frac{z^k}{k!}$}$ auf $ \mbox{$K$}$ gleichmäßig gegen die Exponentialfunktion konvergiert, folgt die Behauptung.