Kompakte Konvergenz.

Kompakte Konvergenz von Funktionenfolgen und -reihen.

In der Funktionentheorie wird meist eine schwächere Bedingung als die gleichmäßige Konvergenz benötigt. Es sei dazu $ \mbox{$D\subseteq\mathbb{C}$}$ offen. Die Funktionenfolge $ \mbox{$(f_n)_{n\ge m}$}$ (bzw. die Funktionenreihe $ \mbox{$\sum_{n=m}^\infty f_n$}$ ) heißt kompakt konvergent auf $ \mbox{$D$}$ , falls eine der beiden folgenden äquivalenten Bedingungen erfüllt ist.

Aufgrund der zweiten Charakterisierung spricht man auch von lokal gleichmäßiger Konvergenz anstelle von kompakter Konvergenz.

Sind alle Funktionen $ \mbox{$f_n:D\to\mathbb{C}$}$ stetig, und ist die Folge $ \mbox{$(f_n)_{n\ge m}$}$ (bzw. die Reihe $ \mbox{$\sum_{n=m}^\infty f_n$}$ ) kompakt konvergent auf $ \mbox{$D$}$ , so ist auch die Grenzfunktion stetig.

Differenzierbarkeit der Grenzfunktion.

Sind alle Funktionen $ \mbox{$f_n:D\to\mathbb{C}$}$ holomorph, und ist die Folge $ \mbox{$(f_n)_{n\ge m}$}$ (bzw. die Reihe $ \mbox{$\sum_{n=m}^\infty f_n$}$ ) kompakt konvergent auf $ \mbox{$D$}$ , so ist auch die Grenzfunktion holomorph, und es gilt

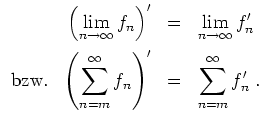
$ \mbox{$\displaystyle \begin{array}{lrcl} &\displaystyle\left(\lim_{n\to\infty... ...fty f_n\right)' &=& \displaystyle\sum_{n=m}^\infty f_n'\right)\;. \end{array}$}$
Kurz: Bei kompakter Konvergenz können die Grenzprozesse Differentiation und Grenzwertbildung vertauscht werden.

Stammfunktion der Grenzfunktion.

Es sei $ \mbox{$G\subseteq\mathbb{C}$}$ ein Gebiet, und $ \mbox{$(f_n)_{n\ge m}$}$ sei eine Folge holomorpher Funktionen $ \mbox{$G\to\mathbb{C}$}$ , welche auf $ \mbox{$G$}$ kompakt konvergiert. Für jedes $ \mbox{$n\ge m$}$ sei eine Stammfunktion $ \mbox{$g_n:G\to\mathbb{C}$}$ gegeben, d.h. $ \mbox{$g_n$}$ ist holomorph und erfüllt $ \mbox{$g_n'=f_n$}$ . Ferner sei $ \mbox{$z_0\in G$}$ derart, daß $ \mbox{$g_n(z_0)$}$ konvergiert für $ \mbox{$n\to\infty$}$ .

Dann konvergiert auch die Folge $ \mbox{$(g_n)_{n\ge m}$}$ kompakt auf $ \mbox{$G$}$ , und es gilt

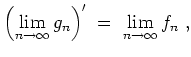
$ \mbox{$\displaystyle \left(\lim_{n\to\infty} g_n\right)' \;=\; \lim_{n\to\infty} f_n\;, $}$
d.h. die Grenzfunktion der Stammfunktionen ist Stammfunktion der Grenzfunktion.

Normale Konvergenz.

Wir geben ein praktisches Kriterium für die kompakte Konvergenz einer Funktionenreihe an.

Es sei zunächst $ \mbox{$\sum_{n=m}^\infty f_n$}$ eine Reihe von Funktionen $ \mbox{$f_n:D\to\mathbb{C}$}$ , wobei $ \mbox{$D\subseteq\mathbb{C}$}$ . Wir sagen, die Reihe $ \mbox{$\sum_{n=m}^\infty f_n$}$ erfüllt den Weierstraßschen $ \mbox{$M$}$ -Test auf $ \mbox{$D$}$ , wenn es eine Folge $ \mbox{$(M_n)_{n\ge m}$}$ positiver reeller Zahlen gibt mit

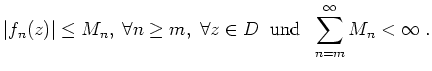
$ \mbox{$\displaystyle \vert f_n(z)\vert\le M_n,\;\forall n\ge m,\; \forall z\in D\;\;\text{und}\;\;\sum_{n=m}^\infty M_n<\infty\;. $}$
In diesem Falle ist die Reihe $ \mbox{$\sum_{n=m}^\infty f_n$}$ gleichmäßig konvergent auf $ \mbox{$D$}$ .

Es sei nun zusätzlich $ \mbox{$D\subseteq\mathbb{C}$}$ offen. Eine Funktionenreihe $ \mbox{$\sum_{n=m}^\infty f_n$}$ von Funktionen $ \mbox{$f_n:D\to\mathbb{C}$}$ heißt normal konvergent auf $ \mbox{$D$}$ , falls eine der beiden folgenden äquivalenten Bedingungen erfüllt ist.

Beachte: Die Majoranten $ \mbox{$M_n$}$ im Weierstraßschen $ \mbox{$M$}$ -Test können dann von den Teilmengen $ \mbox{$K$}$ bzw. $ \mbox{$U$}$ abhängen.

Eine normal konvergente Funktionenreihe ist kompakt konvergent.