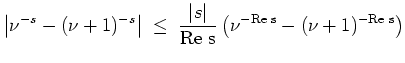Es sei
![]() eine kompakte Teilmenge.
Wir wollen mit dem Cauchy-Kriterium zeigen, daß die Funktionenreihe gleichmäßig auf
eine kompakte Teilmenge.
Wir wollen mit dem Cauchy-Kriterium zeigen, daß die Funktionenreihe gleichmäßig auf
![]() konvergiert.
Es sei dazu
konvergiert.
Es sei dazu
![]() .
.
Da
![]() kompakt ist, gibt es
kompakt ist, gibt es
![]() und
und
![]() mit
mit
Mit abelscher partieller Summation gilt
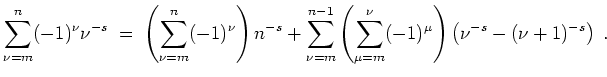
Es sei nun
![]() . Aus
. Aus
![]() ,
,
![]() sowie der Mittelwertungleichung folgt
sowie der Mittelwertungleichung folgt
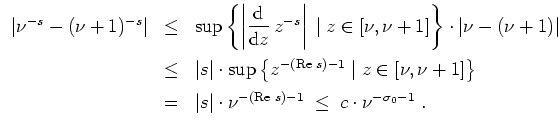
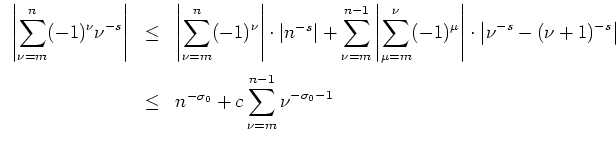
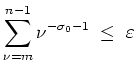
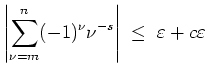
Also ist die Funktionenreihe
![]() auf
auf
![]() gleichmäßig konvergent. Da
gleichmäßig konvergent. Da
![]() beliebig war, konvergiert sie
demnach kompakt auf
beliebig war, konvergiert sie
demnach kompakt auf
![]() .
.
Bemerkung: Mit komplexer Integration und der Dreiecksungleichung für Integrale ergibt sich die bessere Abschätzung