Lösung.

  1. Offenbar ist die leere Summe (d.h. für alle Koeffizienten gilt $ \mbox{$a_\gamma=0$}$ ) ein Element von $ \mbox{$B_1(G)$}$ . Sind $ \mbox{$\Gamma_1=\sum_{\gamma\in W(G)}a_\gamma\gamma$}$ und $ \mbox{$\Gamma_2=\sum_{\gamma\in W(G)}b_\gamma\gamma$}$ Elemente von $ \mbox{$B_1(G)$}$ , so gilt für alle $ \mbox{$z\in\mathbb{C}\setminus G$}$
    $ \mbox{$\displaystyle w(\Gamma_1-\Gamma_2,z) \;=\; w(\Gamma_1,z)-w(\Gamma_2,z) \;=\; 0\;, $}$
    d.h. $ \mbox{$\Gamma_1-\Gamma_2\in B_1(G)$}$ . Somit ist $ \mbox{$B_1(G)$}$ eine Untergruppe von $ \mbox{$Z_1(G)$}$ .
  2. Das Gebiet $ \mbox{$G$}$ ist einfach zusammenhängend genau dann, wenn $ \mbox{$w(\gamma,z)=0$}$ gilt für alle $ \mbox{$\gamma\in W(G)$}$ und alle $ \mbox{$z\in\mathbb{C}\setminus G$}$ , d.h. wenn $ \mbox{$\gamma\in B_1(G)$}$ für alle $ \mbox{$\gamma\in W(G)$}$ . Dies ist äquivalent damit, daß $ \mbox{$B_1(G)=Z_1(G)$}$ , d.h. daß $ \mbox{$H_1(G)$}$ trivial ist.
  3. Es sei $ \mbox{$f:G\to G'$}$ eine konforme Abbildung. Wir definieren eine Abbildung
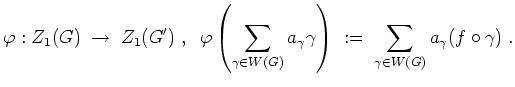
    $ \mbox{$\displaystyle \varphi: Z_1(G)\;\to\; Z_1(G')\;,\;\; \varphi\left(\sum_... ...a_\gamma\gamma\right) \;:=\; \sum_{\gamma\in W(G)}a_\gamma (f\circ\gamma)\;. $}$
    Dabei beachte man, daß $ \mbox{$f\circ\gamma$}$ ein geschlossener Weg in $ \mbox{$G'$}$ ist, für alle $ \mbox{$\gamma\in W(G)$}$ . Wie man leicht nachrechnet, ist $ \mbox{$\varphi$}$ ein Gruppenhomomorphismus.

    Wir wollen nun zeigen, daß $ \mbox{$\varphi(B_1(G))\subseteq B_1(G')$}$ gilt.

    Als Vorbemerkung berechnen wir $ \mbox{$w(f\circ\gamma,z)$}$ für $ \mbox{$\gamma\in K(G)$}$ , etwa $ \mbox{$\gamma:[a,b]\to\mathbb{C}$}$ , und $ \mbox{$z\in\mathbb{C}\setminus G$}$ zu

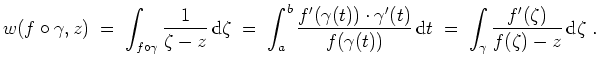
    $ \mbox{$\displaystyle w(f\circ\gamma,z) \;=\; \int_{f\circ\gamma}\dfrac{1}{\ze... ...,\text{d}t \;=\; \int_\gamma \dfrac{f'(\zeta)}{f(\zeta)-z}\,\text{d}\zeta\;. $}$

    Es sei also $ \mbox{$\Gamma=\sum_{\gamma\in W(G)}a_\gamma\gamma\in B_1(G)$}$ . Es sei $ \mbox{$z\in\mathbb{C}\setminus G'$}$ . Dann folgt mit obiger Vorbemerkung

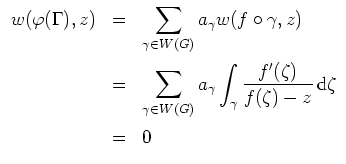
    $ \mbox{$\displaystyle \begin{array}{rcl} w(\varphi(\Gamma),z) &=& \displaysty... ...frac{f'(\zeta)}{f(\zeta)-z}\,\text{d}\zeta\vspace*{2mm}\\ &=& 0 \end{array}$}$
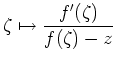    nach der Homologieversion des Cauchyschen Integralsatzes, denn $ \mbox{$\sum_{\gamma\in W(G)} a_\gamma \gamma$}$ ist ein $ \mbox{$G$}$ -nullhomologer Wegezyklus, und die Funktion $ \mbox{$\zeta\mapsto \dfrac{f'(\zeta)}{f(\zeta)-z}$}$ ist holomorph auf $ \mbox{$G$}$ . Somit gilt
    $ \mbox{$\displaystyle \varphi(\Gamma) \;\in\; B_1(G')\;, $}$
    d.h. wir haben $ \mbox{$\varphi(B_1(G))\subseteq B_1(G')$}$ bewiesen.

    Betrachtet man nun statt $ \mbox{$f:G\to G'$}$ die konforme Abbildung $ \mbox{$f^{-1}:G'\to G$}$ , so erhält man analog eine Abbildung $ \mbox{$\tilde{\varphi}:Z_1(G')\to Z_1(G)$}$ , welche invers zu $ \mbox{$\varphi$}$ ist, d.h. es gilt $ \mbox{$\tilde{\varphi}=\varphi^{-1}$}$ und $ \mbox{$\varphi$}$ ist ein Gruppenisomorphismus.

    Aus $ \mbox{$\tilde{\varphi}(B_1(G'))\subseteq B_1(G)$}$ folgt dann

    $ \mbox{$\displaystyle \varphi(B_1(G)) \;=\; B_1(G')\;. $}$
    Aus der Gruppentheorie ist nun bekannt, daß $ \mbox{$\varphi$}$ einen Gruppenisomorphismus
    $ \mbox{$\displaystyle H_1(G) \;=\; Z_1(G)/B_1(G) \;\cong\; Z_1(G')/B_1(G') \;=\; H_1(G') $}$
    induziert.
  4. Es sei $ \mbox{$G':=G\setminus\{z_1,\ldots,z_n\}$}$ . Wir definieren
    $ \mbox{$\displaystyle \psi:Z_1(G')\;\to\; \mathbb{Z}^n\;,\;\; \psi(\Gamma) \;:=\; (w(\Gamma,z_1),\ldots,w(\Gamma,z_n))\;. $}$
    Wie man leicht überprüft, ist $ \mbox{$\psi$}$ ein Gruppenhomomorphismus.

    Wir zeigen nun, daß die Abbildung $ \mbox{$\psi$}$ surjektiv ist. Es sei $ \mbox{$r>0$}$ derart, daß

    $ \mbox{$\displaystyle \overline{B_r(z_1)} \;\subseteq\; G\setminus\{z_2,\ldots,z_n\}\;. $}$
    Dann ist $ \mbox{$\gamma_0:=\partial B_r(z_1)\in Z_1(G')$}$ mit
    $ \mbox{$\displaystyle \psi(\gamma_0) \;=\; (1,0,\ldots,0)\;. $}$
    Analog enthält das Bild von $ \mbox{$\psi$}$ alle Einheitsvektoren und somit auch alle ganzzahligen Linearkombinationen davon. Somit ist $ \mbox{$\psi$}$ surjektiv.

    Wir zeigen nun, daß $ \mbox{$\text{Kern }\psi=B_1(G')$}$ gilt. Ist $ \mbox{$\Gamma\in\text{Kern }\psi$}$ , so folgt $ \mbox{$w(\Gamma,z_\nu)=0$}$ für $ \mbox{$\nu=1,\ldots,n$}$ . Da $ \mbox{$G$}$ einfach zusammenhängend ist, folgt auch $ \mbox{$w(\Gamma,z)=0$}$ für alle $ \mbox{$z\in\mathbb{C}\setminus G$}$ . Insgesamt folgt

    $ \mbox{$\displaystyle w(\Gamma,z)\;=\; 0\;,\;\;\text{f\uml ur alle}\;\; z\in\mathbb{C}\setminus{G'}\;, $}$
    d.h. $ \mbox{$\Gamma\in B_1(G')$}$ . Ist umgekehrt $ \mbox{$\Gamma\in B_1(G')$}$ , so folgt sofort $ \mbox{$w(\Gamma,z_\nu)=0$}$ für $ \mbox{$\nu=1,\ldots,n$}$ , d.h. $ \mbox{$\psi(\Gamma)=0$}$ und $ \mbox{$\Gamma\in\text{Kern }\psi$}$ .

    Damit haben wir gezeigt, daß $ \mbox{$\psi$}$ ein surjektiver Gruppenhomorphismus ist mit $ \mbox{$\text{Kern }\psi=B_1(G')$}$ . Nach dem Homomorphiesatz aus der Gruppentheorie induziert $ \mbox{$\psi$}$ einen Isomorphismus

    $ \mbox{$\displaystyle H_1(G) \;=\; Z_1(G)/B_1(G) \;\cong\; \mathbb{Z}^n\;. $}$
  5. Es sei $ \mbox{$G:=\mathbb{C}\setminus\{0\}$}$ , und $ \mbox{$G':=G\setminus\{1\}=\mathbb{C}\setminus\{0,1\}$}$ . Gäbe es eine konforme Abbildung $ \mbox{$G\to G'$}$ , so wären nach 3. die Gruppen $ \mbox{$H_1(G)$}$ und $ \mbox{$H_1(G')$}$ isomorph. Nach 4. wären demnach die Gruppen $ \mbox{$\mathbb{Z}$}$ und $ \mbox{$\mathbb{Z}^2$}$ isomorph. Dies ist jedoch ein Widerspruch, denn $ \mbox{$\mathbb{Z}$}$ ist zyklisch, während $ \mbox{$\mathbb{Z}^2$}$ nicht zyklisch ist.