Unendliche Produkte.

Konvergenz unendlicher Produkte.

Es sei $ \mbox{$(a_n)_{n\ge m}$}$ eine Folge komplexer Zahlen. Das unendliche Produkt $ \mbox{$\prod_{n=m}^\infty a_n$}$ heißt konvergent, falls es ein $ \mbox{$n_0\ge m$}$ gibt derart, daß

$ \mbox{$\displaystyle a_n\;\ne\; 0\;,\;\;\text{f\uml ur alle}\;\; n\;\ge\;n_0\... ...t{und}\;\;\lim_{N\to\infty}\prod_{n=n_0}^N a_n\;\ne\;0 \;\;\text{existiert.} $}$
In diesem Falle heißt
$ \mbox{$\displaystyle \prod_{n=m}^\infty a_n \;:=\; \lim_{N\to\infty}\prod_{n=m}^N a_n $}$
der Wert des unendlichen Produktes.

Man beachte, daß die bloße Konvergenz der Folge der Partialprodukte $ \mbox{$\left(\prod_{n=m}^N a_n\right)_{N\ge m}$}$ nicht für die Konvergenz des unendlichen Produktes hinreichend ist. Zum Beispiel konvergieren die Partialprodukte des unendlichen Produktes $ \mbox{$\prod_{n=1}^\infty\frac{1}{n}$}$ gegen $ \mbox{$0$}$ , aber das unendliche Produkt $ \mbox{$\prod_{n=1}^\infty\frac{1}{n}$}$ konvergiert nicht.

Die Motivation für diese Definition der Konvergenz ist folgende Tatsache: Konvergiert das unendliche Produkt $ \mbox{$\prod_{n=m}^\infty a_n$}$ , so gilt

$ \mbox{$\displaystyle \prod_{n=m}^\infty a_n \;=\; 0 \;\;\iff\;\; \exists n\ge m:\; a_n=0\;. $}$

Das notwendige Kriterium besagt, falls das unendliche Produkt $ \mbox{$\prod_{n=m}^\infty a_n$}$ konvergiert, so gilt für die Faktorenfolge $ \mbox{$a_n\to 1$}$ für $ \mbox{$n\to\infty$}$ .

Logarithmuskriterium.

Es sei $ \mbox{$(a_n)_{n\ge m}$}$ eine Folge komplexer Zahlen. Dann sind folgende Aussagen äquivalent.

Und im Falle der Konvergenz gilt
$ \mbox{$\displaystyle \begin{array}{rcl} \displaystyle\prod_{n=m}^\infty a_n ... ...a_n+2\pi\text{i}k\;,\;\;\text{f\uml ur ein}\;\; k\in\mathbb{Z}\;. \end{array}$}$

Absolute Konvergenz.

Es sei wieder $ \mbox{$(a_n)_{n\ge m}$}$ eine Fogle komplexer Zahlen. Wir betrachten in diesem Abschnitt das unendliche Produkt $ \mbox{$\prod_{n=m}^\infty(1+a_n)$}$ . Das notwendige Kriterium für die Konvergenz sagt für diesen Fall aus, daß $ \mbox{$a_n\to 0$}$ für $ \mbox{$n\to\infty$}$ .

Das unendliche Produkt $ \mbox{$\prod_{n=m}^\infty(1+a_n)$}$ heißt absolut konvergent, falls das unendliche Produkt $ \mbox{$\prod_{n=m}^\infty(1+\vert a_n\vert)$}$ konvergiert.

Folgende Aussagen sind äquivalent:

Aus der absoluten Konvergenz eines unendlichen Produktes folgt stets die gewöhnliche Konvergenz.

Ein absolut konvergentes unendliches Produkt $ \mbox{$\prod_{n=m}^\infty(1+a_n)$}$ ist auch unbedingt konvergent, d.h. sind $ \mbox{$k,m\in\mathbb{Z}$}$ und ist $ \mbox{$\varphi:\{k,k+1,\ldots\}\to\{m,m+1,\ldots\}$}$ eine bijektive Abbildung, so ist auch die Umordnung $ \mbox{$\prod_{n=k}^\infty a_{\varphi(n)}$}$ konvergent, und es gilt

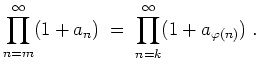
$ \mbox{$\displaystyle \prod_{n=m}^\infty (1+a_n) \;=\; \prod_{n=k}^\infty (1+a_{\varphi(n)})\;. $}$

Normale Konvergenz unendlicher Produkte.

Es sei $ \mbox{$G\subseteq\mathbb{C}$}$ , und $ \mbox{$(f_n)_{n\ge m}$}$ sei eine Folge von Funktionen $ \mbox{$f_n:G\to\mathbb{C}$}$ . Das unendliche Produkt $ \mbox{$\prod_{n=m}^\infty (1+f_n)$}$ heißt normal konvergent auf $ \mbox{$G$}$ , falls die Funktionenreihe $ \mbox{$\sum_{n=m}^\infty f_n$}$ normal auf $ \mbox{$G$}$ konvergiert.

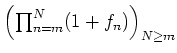Ist das unendliche Produkt $ \mbox{$\prod_{n=m}^\infty (1+f_n)$}$ normal konvergent auf $ \mbox{$G$}$ , so konvergiert die Funktionenfolge der Partialprodukte $ \mbox{$\left(\prod_{n=m}^N(1+f_n)\right)_{N\ge m}$}$ kompakt auf $ \mbox{$G$}$ , und für alle $ \mbox{$z\in G$}$ ist das unendliche Produkt $ \mbox{$\prod_{n=m}^\infty (1+f_n(z))$}$ absolut konvergent.