(Der Satz von Hurwitz)
Es sei
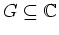 ein Gebiet, und es sei
ein Gebiet, und es sei
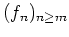 eine Folge holomorpher Funktionen
eine Folge holomorpher Funktionen
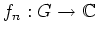 , welche auf
, welche auf
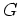 kompakt gegen
kompakt gegen
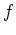 konvergiert. Zeige.
konvergiert. Zeige.
- Es seien
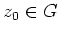 und
und
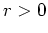 derart, daß
derart, daß
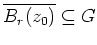 und
und
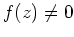 für alle
für alle
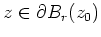 . Dann gibt es ein
. Dann gibt es ein
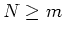 derart, daß für alle
derart, daß für alle
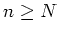 die Fuktionen
die Fuktionen
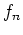 und
und
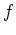 gleich viele Nullstellen (mit Vielfachheiten) in
gleich viele Nullstellen (mit Vielfachheiten) in
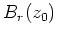 haben.
haben.
- Es gelte
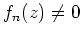 für alle
für alle
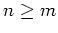 und alle
und alle
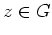 . Dann ist entweder
. Dann ist entweder
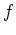 identisch
identisch
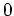 oder
oder
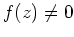 für alle
für alle
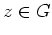 .
.
- Es sei
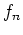 injektiv für alle
injektiv für alle
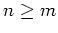 . Dann ist
. Dann ist
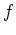 konstant oder injektiv auf
konstant oder injektiv auf
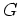 .
.
![]() ein Gebiet, und es sei
ein Gebiet, und es sei
![]() eine Folge holomorpher Funktionen
eine Folge holomorpher Funktionen
![]() , welche auf
, welche auf
![]() kompakt gegen
kompakt gegen
![]() konvergiert. Zeige.
konvergiert. Zeige.