Hinweis.

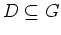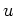  1. Auf jeder offenen Kreisscheibe $ \mbox{$D\subseteq G$}$ ist $ \mbox{$u$}$ der Realteil einer holomorphen Funktion.

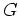  2. Beweise zunächst, daß die Behauptung gilt, wenn $ \mbox{$G$}$ eine offene Kreisscheibe ist. Betrachte im allgemeinen Fall die Menge
    $ \mbox{$\displaystyle U \;:=\; \{z\in G\;\vert\; \exists\varepsilon>0\;:\; u(s)=v(s)\;,\;\;\text{f\uml ur alle}\;\;s\in B_\varepsilon(z)\}\;, $}$
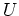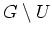    und zeige, daß sowohl $ \mbox{$U$}$ als auch $ \mbox{$G\setminus U$}$ offen sind.

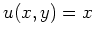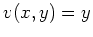  3. Betrachte $ \mbox{$u(x,y)=x$}$ und $ \mbox{$v(x,y)=y$}$ .

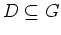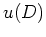  4. Zeige, daß für jede offene Kreisscheibe $ \mbox{$D\subseteq G$}$ die Menge $ \mbox{$u(D)$}$ offen ist. Verwende dazu den Identitätssatz für harmonische Funktionen und den Satz von der Gebietstreue holomorpher Funktionen.

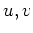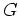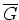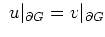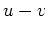  5. Sind $ \mbox{$u,v$}$ harmonisch auf $ \mbox{$G$}$ , stetig auf $ \mbox{$\overline{G}$}$ mit $ \mbox{$\ u\vert _{\partial G} = v\vert _{\partial G}$}$ , so wende das Maximumprinzip auf $ \mbox{$u-v$}$ an.