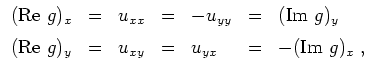Wir betrachten die Funktion
für
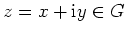 .
Dann sind
.
Dann sind
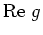 und
und
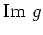 differenzierbar, und es gilt
d.h.
differenzierbar, und es gilt
d.h.
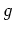 erfüllt die Cauchy-Riemannschen Differentialgleichungen und ist somit holomorph auf
erfüllt die Cauchy-Riemannschen Differentialgleichungen und ist somit holomorph auf
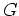 .
Da
.
Da
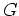 einfach zusammenhängend ist, besitzt
einfach zusammenhängend ist, besitzt
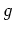 eine Stammfunktion
eine Stammfunktion
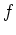 .
Es gilt folglich
Daher sind
.
Es gilt folglich
Daher sind
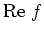 und
und
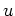 differenzierbare Funktionen auf
differenzierbare Funktionen auf
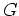 , deren Gradienten übereinstimmen, d.h.
sie unterscheiden sich um eine Konstante
, deren Gradienten übereinstimmen, d.h.
sie unterscheiden sich um eine Konstante
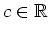 . Dann ist
. Dann ist
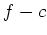 holomorph auf
holomorph auf
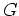 und
und
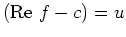 .
.