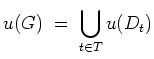Bemerkung: Es ist auch möglich, aber weit aufwendiger, die Laplacesche Differentialgleichung für
![]() nachzurechnen.
nachzurechnen.
![]() Sind
Sind
![]() offene Kreisscheiben mit
offene Kreisscheiben mit
![]() , und gilt
, und gilt
![]() ,
so folgt daraus
,
so folgt daraus
![]() .
.
Es gibt nämlich holomorphe Funktionen
![]() mit
mit
![]() und
und
![]() .
Dann ist
.
Dann ist
![]() holomorph und erfüllt auf
holomorph und erfüllt auf
![]() die Gleichung
die Gleichung
Es sei nun
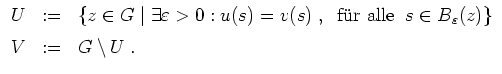
Wir wollen zeigen, daß
![]() ebenfalls offen ist.
Es sei
ebenfalls offen ist.
Es sei
![]() . Es sei
. Es sei
![]() so gewählt, daß
so gewählt, daß
![]() .
Wir wollen zeigen, daß
.
Wir wollen zeigen, daß
Damit haben wir bewiesen, daß
![]() offen ist. Ferner ist
offen ist. Ferner ist
![]() , da nach Voraussetzung
, da nach Voraussetzung
![]() . Da
. Da
![]() zusammenhängend ist, folgt
daraus
zusammenhängend ist, folgt
daraus