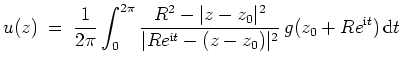Das Dirichletsche Randwertproblem.

Es sei $ \mbox{$D\subseteq\mathbb{C}$}$ eine offene Kreisscheibe, und es sei $ \mbox{$g:\partial D\to\mathbb{R}$}$ eine stetige Funktion. Dann gibt es genau eine stetige Funktion $ \mbox{$u:\overline{D}\to\mathbb{C}$}$ mit

Man sagt, das Dirichletsche Randwertproblem ist für Kreisscheiben lösbar, d.h. jede stetige Randwertverteilung läßt sich (eindeutig) stetig zu einer im Inneren harmonischen Funktion fortsetzen.

Ist etwa $ \mbox{$D=B_R(z_0)$}$ , so gewinnt man $ \mbox{$u$}$ mit Hilfe der Poissonschen Integralformel, d.h. es gilt

$ \mbox{$\displaystyle u(z) \;=\; \frac{1}{2\pi}\int_0^{2\pi} \frac{R^2-\vert z... ...^2}{\vert Re^{\text{i}t}-(z-z_0)\vert^2}\, g(z_0+Re^{\text{i}t})\,\text{d}t $}$
für alle $ \mbox{$z\in B_R(z_0)$}$ .