Jacobi solver for boundary value problems

Content

Transfer of self-defined data types using MPI
Sample solution
Transfer of matrices using MPI
Sample solution
Boundaries and extent of an MPI data type
Sample solution
Jacobi solver for boundary value problems
- Exercise
- Compilation and execution
Sample solution

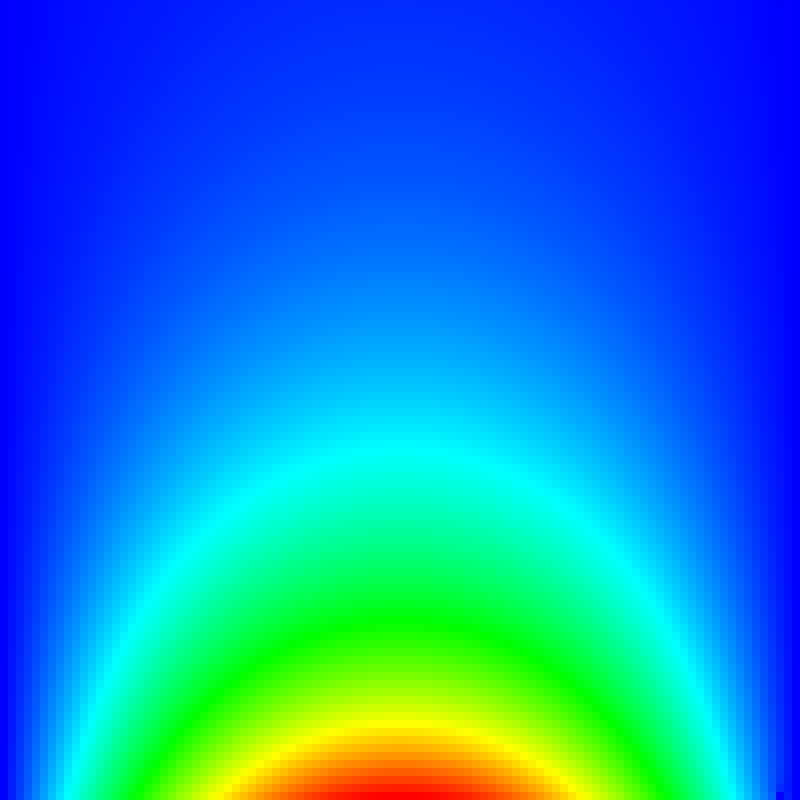
We are looking for a numerical approximation of the function $u(x,y)$ f where $u_{xx} + u_{yy} = 0$ with the boundary equation $u(x,y) = g(x,y)$ for $x, y \in \delta\Omega$. The image above presents a numerical approximation for the boundary conditions $u(x,0) = sin(\pi x)$, $u(x,1) = sin(\pi x) e^{-\pi}$ und $u(0, y) = u(1, y) = 0$.

The problem can be solved numerically by dividing the domain $\Omega$ uniformely by using a $N \times N$ grid. Then $u(x,y)$ can be represented on the points of the grid using a matrix $A$ where $A_{i,j} = u\left(\frac{i}{N}, \frac{j}{N}\right)$ for $i,j = 0 \dots N$:

\[ \left( \begin{array}{ccccc} A_{0,N-1} & A_{1,N-1} & \dots & A_{N-2, N-1} & A_{N-1,N-1} \\ A_{0,N-2} & A_{1,N-2} & \dots & A_{N-2, N-2} & A_{N-1,N-2} \\ \vdots & \vdots & & \vdots & \vdots \\ A_{0,1} & A_{1,1} & \dots & A_{N-2, 1} & A_{N-1, 1} \\ A_{0,0} & A_{1,0} & \dots & A_{N-2, 0} & A_{N-1, 0} \end{array} \right)\]

A stepwise approximation of $A$ can be done by computing a sequence of $A_0$, $A_1 \dots$ where the border of $A_0$ is defined by $g(x,y)$ and otherwise initialized to zeroes.

Multiple iterative solvers are possible. The simplest is the Jacobi solver that works with a 5-point difference star:

\[ A_{{k+1}_{i,j}} = \frac{1}{4} \left( A_{k_{i-1,j}} + A_{k_{i,j-1}} + A_{k_{i,j+1}} + A_{k_{i+1,j}} \right)\]

for $i, j \in 1 \dots N-1, k = 1, 2, \dots$. (See Alefeld et al, Parallele numerische Verfahren, pp. 18.)

The iterations are repeated until

\[ \max_{i,j = 1 \dots N-1} \left| A_{{k+1}_{i,j}} - A_{{k}_{i,j}} \right| \le \epsilon\]

for some given value of $\epsilon$.

Exercise

Start with the development of a non-parallelized version for the Jacobi solver. If you work with the dimensions $100 \times 100$ you will need slightly more than 5,000 Jacobi iterative steps for $\epsilon = 10^{-6}$.

You can visualize your result by creating a JPEG file jacobi.jpg as follows:
```
#include <hpc/matvec/matrix2pixbuf.hpp>
#include <hpc/aux/hsvcolor.hpp>

/* ... */

auto pixbuf = create_pixbuf(A, [](double val) -> HSVColor<double> {
   return HSVColor<double>((1-val) * 240, 1, 1);
}, 8);
gdk_pixbuf_save(pixbuf, "jacobi.jpg", "jpeg", nullptr,
   "quality", "100", nullptr);
```
You will need the additional flags $(pkg-config --cflags gdk-pixbuf-2.0) for compiling and $(pkg-config --libs gdk-pixbuf-2.0) for linking.
Parallelize the Jacobi solver by dividing the matrix in groups of rows among the available processes. Then the processes need to exchange their border rows with the respective neighbor processes.

Assume $A$ is of dimensions $11 \times 11$ and we have three processes. Then each of the three processes has to compute three rows during each iterative step (note that the border remains unchanged). Then you would need following transfers between the processes $P_1$, $P_2$ and $P_3$ in each step:
- $P_1 \longrightarrow P_2: A_{3,1} \dots A_{3,9}$
- $P_2 \longrightarrow P_3: A_{6,1} \dots A_{6,9}$
- $P_3 \longrightarrow P_2: A_{7,1} \dots A_{7,9}$
- $P_2 \longrightarrow P_1: A_{4,1} \dots A_{4,9}$
Processes responsible for inner partitions send and receive two inner rows of $A$. The border processes send and receive just one row.

You can do this in each process with two calls of MPI_Sendrecv, an operation that combines MPI_Send and MPI_Recv where both operations run in parallel:
```
int MPI_Sendrecv(const void* sendbuf, int sendcount, MPI_Datatype sendtype,
                 int dest, int sendtag,
                 void* recvbuf, int recvcount, MPI_Datatype recvtype,
                 int source, int recvtag,
                 MPI_Comm comm, MPI_Status* status);
```
The border processes are free to use MPI_PROC_NULL for dest and source if there is no neighbor. MPI_PROC_NULL is the null process. A communication with the null process does not take place. Using this approach you could in a first phase transfer rows from higher ranked processes to lower ranked processes and subsequently in the second phase transfer rows from lower ranked processes to higher ranked processes.

At the beginning it is best to configure a fixed number of steps to avoid the non-trivial test whether we can stop.

To compute the global maxium, it is recommended to use a combination of MPI_Reduce and MPI_Bcast. Using MPI_Reduce the process with rank 0 learns the global maximum which can be subsequently broadcast to all processes using the MPI_Bcast operation.

int MPI_Reduce(const void* sendbuf, void* recvbuf, int count,
               MPI_Datatype datatype, MPI_Op op, int root,
               MPI_Comm comm);
int MPI_Bcast(void* buffer, int count, MPI_Datatype datatype,
              int root, MPI_Comm comm);

In this case MPI_MAX is to be used for op.

Compilation and execution

theon$ mpic++ -g -O3 -std=c++17 \
>    -Istep03 -I/home/numerik/pub/pp/ss19/lib \
>    $(pkg-config --cflags gdk-pixbuf-2.0) \
>    -o jacobi jacobi.cpp $(pkg-config --libs gdk-pixbuf-2.0)
theon$ mpirun -np 4 ./jacobi
5090 iterations
theon$