Prof. Dr. Franz Schweiggert und Dr. Johannes Mayer Abt. Angewandte
Informationsverarbeitung
Ralph Guderlei Blatt 1 - 28. April 2006
[c]
Software Engineering Praxis (SS 2006)
Abgabetermin: 05. Mai 2006
Schon seit der Antike gibt es Verfahren um die Kreiszahl 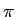 näherungsweise zu bestimmen.
Ein klassischer Ansatz ist die Flächenformel.
Bei der Flächenformel wird ausgenutzt, dass
näherungsweise zu bestimmen.
Ein klassischer Ansatz ist die Flächenformel.
Bei der Flächenformel wird ausgenutzt, dass 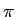 nur zur Berechnung der Kreisfläche, aber nicht zur Berechnung
der Fläche des den Kreis einschließenden Quadrats benötigt wird. Sei
nur zur Berechnung der Kreisfläche, aber nicht zur Berechnung
der Fläche des den Kreis einschließenden Quadrats benötigt wird. Sei 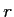 nun der Radius eines Kreises, dann ergibt sich
nun der Radius eines Kreises, dann ergibt sich
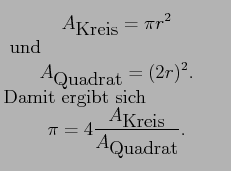
Die Fläche des Quadrats kann direkt berechnet werden, die Fläche des Kreises kann näherungsweise durch
Auszählen der Punkte 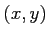 bestimmt werden, die im Kreis liegen. Um diese Punkte zu zählen kann man ein Koordinatensystem
mit
bestimmt werden, die im Kreis liegen. Um diese Punkte zu zählen kann man ein Koordinatensystem
mit
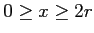 und
und
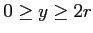 konstruieren, dessen Mitte in
konstruieren, dessen Mitte in 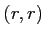 liegt. Für alle Punkte im Kreis gilt dann
liegt. Für alle Punkte im Kreis gilt dann
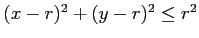 .
.
Um ein brauchbares Ergebnis zu erhalten sollte 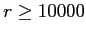 gewählt werden.
gewählt werden.
Die Bailey-Borwein-Plouffe-Formel ist eine relativ neue Darstellung von 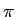 als Reihe:
als Reihe:
Mit dieser Formel können beliebige Stellen von 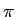 bestimmt werden, ohne die vorhergehenden Stellen berechnen zu müssen.
Die Zahl
bestimmt werden, ohne die vorhergehenden Stellen berechnen zu müssen.
Die Zahl 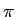 kann durch Abbrechen der Reihe nach
kann durch Abbrechen der Reihe nach 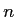 Summationen näherungsweise berechnet werden.
Summationen näherungsweise berechnet werden.
Implementieren Sie beide Methoden zur näherungsweisen Berechung von 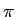 . Vergleichen die Ergebnisse der beiden Methoden mit
der in Java vorgehaltenene Konstante Math.PI. Welche Aussage können Sie über die Laufzeit der beiden Methoden machen?
. Vergleichen die Ergebnisse der beiden Methoden mit
der in Java vorgehaltenene Konstante Math.PI. Welche Aussage können Sie über die Laufzeit der beiden Methoden machen?
Um den ggT zweier Integer-Werte a, b zu bestimmen, wird häufig der Euklidsche Algorithmus
verwendet. Eine Variante ist der sog. ''binäre Euklidsche Algorithmus'':
- setze m = a, n = b
- dividiere m und n durch 2 solange, bis eine der beiden Zahlen ungerade ist. Die Zahl der notwendigen
Divisionsschritte sei k. Falls n gerade ist, vertausche m und n.
- dividiere m durch 2, bis m ungerade ist
- ist m<n, so vertausche diese Zahlen
- setze m = m - n
- ist m
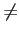 0, dann fahre fort mit Schritt 3.
0, dann fahre fort mit Schritt 3.
- ggT(a,b) = n
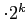
Implementieren Sie den binären Euklidschen Algorithmus in Java.
Viel Erfolg!
Ralph Guderlei
2006-04-28
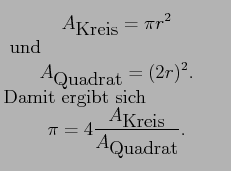
![\includegraphics[width=6cm]{Flaechenformel}](img4.png)
![]() bestimmt werden, die im Kreis liegen. Um diese Punkte zu zählen kann man ein Koordinatensystem
mit
bestimmt werden, die im Kreis liegen. Um diese Punkte zu zählen kann man ein Koordinatensystem
mit
![]() und
und
![]() konstruieren, dessen Mitte in
konstruieren, dessen Mitte in ![]() liegt. Für alle Punkte im Kreis gilt dann
liegt. Für alle Punkte im Kreis gilt dann
![]() .
.
![]() gewählt werden.
gewählt werden.
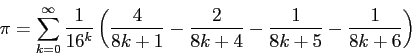
![]() . Vergleichen die Ergebnisse der beiden Methoden mit
der in Java vorgehaltenene Konstante Math.PI. Welche Aussage können Sie über die Laufzeit der beiden Methoden machen?
. Vergleichen die Ergebnisse der beiden Methoden mit
der in Java vorgehaltenene Konstante Math.PI. Welche Aussage können Sie über die Laufzeit der beiden Methoden machen?