Prof. Dr. Franz Schweiggert Abteilung Angewandte Informationsverarbeitung 01.02.2006
Norbert Heidenbluth Blatt 14






Allgemeine Informatik I für Mathematiker/Wirtschaftsmathematiker
(WS 2005/2006)


Abgabetermin: 08. Februar 2006

In diesem Übungsblatt geht es um Rekursionen. Es ist gegliedert in drei (nicht aufeinander aufbauende) Aufgaben, die hier ihrem Schwierigkeitsgrad nach geordnet sind. Aufgabe 27 ist sehr stark an das Fibonacci-Beispiel (vgl. Übungen am 01.02.2006) angelehnt und soll nochmals das Prinzip der Rekursion verdeutlichen. Aufgabe 28 führt in die wechselseitig rekursiven Funktionen ein, und in Aufgabe 29 gilt es dann, sich die zur Problemlösung notwendige Rekursion selbst zu überlegen.

Aufgabe 27: Die Q-Sequenz (2 Punkte)

Die ``Meta-Fibonacci-Zahlen'' von Hofstadter (auch genannt: die ``Q-Sequenz'') stellen eine Erweiterung der Idee der Fibonacci-Zahlen dar. Auch hier ergeben sich die Folgeglieder durch Addition zweier vorausgegangener Glieder, allerdings nicht - wie bei den Fibonacci-Zahlen - der unmittelbar vorausgegangenen.

Lange Rede, kurzer Sinn -- die Bildungsvorschrift für die Meta-Fibonacci-Zahlen lautet wie folgt:

$$Q(n) = \left\{ \begin{array} {c@{\quad \mbox{f\uml {u}r }}l}... ...n-2)) & n \in \mathbb{N}\setminus \{1,2\} \end{array} \right.$$

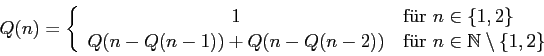
Schreiben Sie ein Java-Programm, das eine Unter- und eine Obergrenze einliest und für alle $\mathbb{N}$ in diesem Intervall $Q(n)$ rekursiv berechnet und ausgibt.

Aufgabe 28: Die Male-Female-Folge (4 Punkte)

Nach Aufgabe 27 finden Sie Hofstadter ganz toll? Und außerdem sind Sie begeisterte Verfechterin der Gleichberechtigung der Geschlechter? Und Rekursionen sind mittlerweile Ihr Lebensinhalt geworden? Prima, dann wird Ihnen diese Aufgabe auch gefallen:

Die sog. ``Male-Female-Folge'' von Hofstadter ist wie folgt definiert:

$$\begin{eqnarray*} F(0) & = & 1 \\ M(0) & = & 0 \\ F(n) & = & n - M(F(n-1)) \\ M(n) & = & n - F(M(n-1)) \\ \end{eqnarray*}$$

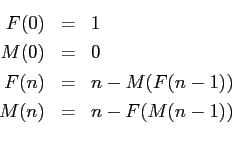
Schreiben Sie (mal wieder) ein Java-Programm, das genau wie in der Aufgabe zuvor eine Unter- und eine Obergrenze einliest und für alle $\mathbb{N}$ dieses Intervall dann jeweils die Funktionswerte von $F(n)$ und $M(n)$ (rekursiv) berechnet und ausgibt.

Tip:

Um den Arbeitsaufwand gering zu halten, können Sie hier selbstverständlich Ihre Lösung aus Aufgabe 27 wiederverwerten, indem Sie lediglich die Methode(n) verändern bzw. ergänzen.

Aufgabe 29: Vom Paarungsverhalten der Dackel (9 Pkt.)

Ihre kleine Schwester wünscht sich nichts sehnlicher als einen Hund, am besten einen Rauhhaardackel. Sie sind allerdings gegen einen Kläffer im Haus, denn der würde Sie mit seinem Bellen nur in der Konzentration auf Ihre Informatik-Übungen stören.

Deshalb beschließen Sie, Ihre kleine Schwester mit einer abenteuerlichen Geschichte von der ungezügelten Vermehrung der Dackel von diesem Wunsch abzubringen und erzählen Ihr etwas vom Paarungsverhalten der Dackel:

Rauhhaardackel

paaren sich im Alter von 6 Jahren und von 8 Jahren derart, daß sie einen kleinen Kurzhaardackel hervorbringen, und nach 7 bzw. 9 Jahren schenken sie jeweils einem neuen Rauhhaardackel das Leben. Im Alter von 12 Jahren sterben sie dann.

Kurzhaardackel

vermehren sich einmal im Alter von 5 Jahren und einmal im Alter von 6 Jahren, und in beiden Fällen entsteht jeweils ein Langhaardackel. Wenn ein Kurzhaardackel 10 Jahre alt ist, so tritt er ab von der Lebensbühne.

Langhaardackel

sind im Alter von 4 Jahren und von 5 Jahren recht umtriebig und erzeugen jeweils ein Zwillingspaar Rauhhaardackel. Mit 9 Jahren zeugen sie noch einen Kurzhaardackel, und mit 15 Jahren dackeln sie ab.

Aus Sicht der Biologie ist das sicherlich hanebüchener Unfug, aber das merkt Ihre kleine Schwester noch nicht. Stattdessen möchte sie wissen, wieviele verschiedene Dackel (detailliert aufgelistet nach Sorte) sie wohl in $n$ Jahren zu füttern und auszuführen hätte und bittet Sie daher:

``Schreibe mir doch bitte ein Java-Programm, dem ich als Eingabe die Anzahl von Jahren ($n$) gebe, und das mir ausgibt, wieviele Tiere der jeweiligen Dackelsorte in $n$ Jahren leben werden -- davon ausgehend, daß ich einen (neugeborenen) Rauhhaardackel geschenkt bekomme und sich dieser so paaren kann und wird, wie Du mir es zuvor beschrieben hast.''

Beispiel:

theseus$ java Dackel 
Fuer welche Anzahl von Jahren wollen wir das Dackelleben simulieren?
20
Nach 20 Jahren leben:
   21 Rauhhaardackel, 
   6 Kurzhaardackel und 
   8 Langhaardackel.

Nach erfolgreicher Arbeit bekommen Sie von Ihrem Tutor entweder bis zu 9 Punkte, eventuell aber auch bis zu 9 Dackel (Verhandlungssache).

P.S.: Ihre kleine Schwester möchte jetzt doch lieber eine Katze haben$\ldots$!

Viel Erfolg!