Dr. Andreas Borchert Institut für Angewandte
Informationsverarbeitung 28. November 2006
Christian Ehrhardt Blatt 6

Allgemeine Informatik III (WS 2006/2007)
Abgabetermin 5.Dezember 2006
In dieser Aufgabe wird ein Programm entwickelt, das in einem
Graph die Länge des kürzesten Wegs vom Startknoten (bei uns
immer der mit der Nummer 0) zu allen
anderen Knoten berechnet. Für die Zwecke dieser Aufgabe besteht
ein Graph aus 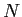 Knoten, die von 0 bis
Knoten, die von 0 bis 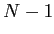 durchnumeriert sind.
Von einem Knoten zu einem anderen kann es entweder eine direkte
Verbindung der Länge 1 oder keine direkte Verbindung geben.
durchnumeriert sind.
Von einem Knoten zu einem anderen kann es entweder eine direkte
Verbindung der Länge 1 oder keine direkte Verbindung geben.
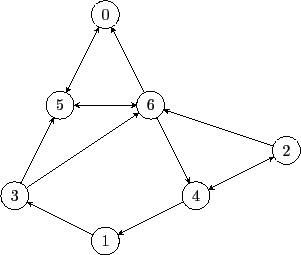
Achtung: Eine solche Verbindung funktioniert nur in eine
Richtung, es kann also durchaus sein, daß man (wie im unten gezeigten
Beispiel) von Knoten 3 über eine direkte Verbindung zu Knoten 5
kommen kann, aber nicht von Knoten 5 über eine direkte Verbindung
zu Knoten 3. Natürlich ist es aber auch möglich, daß zwischen zwei
Knoten je eine direkte Verbindung in die eine und eine in die andere
Richtung gibt (im Beispiel zwischen den Knoten 5 und 6 der Fall).
Die folgende Abbildung zeigt einen Graph mit 7 Knoten. Die
Pfeilspitzen zeigen an, in welche Richtung die jeweiligen
Kanten als direkte Verbindung zwischen Knoten benutzt werden
können.
Wenn wir, wie immer in dieser Aufgabe, den Knoten 0 als Startknoten
wählen, dann ergeben sich die folgenden Längen für die kürzesten
Wege:
| Nummer des Knotens |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
| Länge des kürzesten Wegs von 0 aus |
0 |
4 |
4 |
5 |
3 |
1 |
2 |
Ein Graph wird durch folgende Informationen vollständig
beschrieben:
- Die Anzahl
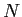 der Knoten im Graph (durchnumeriert
beginnend bei 0)
der Knoten im Graph (durchnumeriert
beginnend bei 0)
- Eine
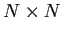 -Matrix aus Nullen und Einsen, wobei der
Eintrag an der Stelle
-Matrix aus Nullen und Einsen, wobei der
Eintrag an der Stelle 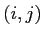 genau dann eine Eins ist,
wenn es eine direkte Verbindung von Knoten
genau dann eine Eins ist,
wenn es eine direkte Verbindung von Knoten 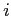 zu Knoten
zu Knoten 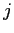 gibt.
gibt.
Eine solche Beschreibung des oben abgebildeten Graphen könnte
also wie folgt aussehen:
7
0000010
0001000
0000101
0000011
0110000
1000001
1000110
Euer Programm soll eine solche Beschreibung eines Graphen von der
Standardeingabe einlesen können.
Bei der Berechnung des kürzesten Weges geht man z.B. wie folgt
vor:
- Eine Zahl, die als Abstand nicht vorkommen kann
(z.B. die -1), wird für einen unendlichen Abstand
reserviert. Am Ende hat ein Knoten von 0 den Abstand
unendlich, wenn es keinen Pfad von Knoten 0 zu diesem Knoten
gibt.
- Zu Beginn hat der Knoten 0 den Abstand 0 von Knoten 0
(wer hätte es gedacht). Alle anderen Knoten haben
zu Beginn den Abstand unendlich von Knoten 0.
- In jedem Schritt wird ein Knoten gewählt, der von den
bisher noch nicht gewählten Knoten den minimalen Abstand von
Knoten 0 hat. Knoten mit Abstand unendlich können nicht
ausgewählt werden. Damit wird jeder Knoten höchstens ein
einziges Mal ausgewählt und im ersten Schritt kann nur der
Knoten 0 gewählt werden, weil alle anderen den Abstand
unendlich haben.
- Wurde ein Knoten gewählt, dann betrachtet man alle
Nachbarknoten, die vom gewählten Knoten aus über eine
direkte Verbindung erreichbar sind. Alle unter diesen Knoten,
die bisher noch den Abstand unendlich haben, bekommen jetzt
einen neue Abstand zugewiesen. Dieser Abstand ist um genau 1
größer, als der Abstand des gewählten Knoten.
- Es wird so lange ein neuer Knoten ausgewählt, bis
jeder Knoten einmal gewählt wurde oder bis alle noch nicht
gewählten Knoten den Abstand unendlich haben.
Für den oben gezeigten Graph würde der Algorithmus also wie folgt
ablaufen:
| |
Abstand von 0 zu Knoten |
|
| |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
gewählter Knoten |
| Schritt 0 |
0 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
0 |
| Schritt 1 |
0 |
-1 |
-1 |
-1 |
-1 |
1 |
-1 |
5 |
| Schritt 2 |
0 |
-1 |
-1 |
-1 |
-1 |
1 |
2 |
6 |
| Schritt 3 |
0 |
-1 |
-1 |
-1 |
3 |
1 |
2 |
4 |
| Schritt 4 |
0 |
4 |
4 |
-1 |
3 |
1 |
2 |
2 (nichts zu ändern!) |
| Schritt 5 |
0 |
4 |
4 |
-1 |
3 |
1 |
2 |
1 |
| Schritt 6 |
0 |
4 |
4 |
5 |
3 |
1 |
2 |
3 (nichts zu ändern!) |
| Schritt 7 |
0 |
4 |
4 |
5 |
3 |
1 |
2 |
Ende |
Natürlich interessiert uns eigentlich nicht nur die Länge des
kürzesten Wegs sondern auch ein möglicher kürzester Weg selbst.
Zum Glück kann man diesen aus dem Graph und den Längen der kürzesten
Wege wieder rekonstruieren. Dazu beginnt man beim Zielknoten und
betrachtet alle Vorgänger, also alle Knoten, von denen es eine
direkte Verbindung zum Zielknoten gibt. Einer dieser Knoten muß
von Knoten 0 aus über einen Pfad erreichbar sein, der um 1 kürzer
ist, als der kürzeste Pfad zum Zielknoten. Ein kürzester Pfad
zum Zielknoten setzt sich dann aus diesem Pfad und der direkten
Verbindung zusammen.
Ergänzen Sie Ihr Programm so, daß neben der Länge der kürzesten Wege
auch noch die Wege selbst ausgegeben werden. Eine vollständige
Ausgabe für das oben angegebene Beispiel könnte also wie folgt
aussehen:
Dist from 0 to 0: 0 Path: 0
Dist from 0 to 1: 4 Path: 0 5 6 4 1
Dist from 0 to 2: 4 Path: 0 5 6 4 2
Dist from 0 to 3: 5 Path: 0 5 6 4 1 3
Dist from 0 to 4: 3 Path: 0 5 6 4
Dist from 0 to 5: 1 Path: 0 5
Dist from 0 to 6: 2 Path: 0 5 6
- Auf der Homepage der Vorlesung gibt es weitere Beispiele
von Graphen. Selbstverständlich sollte Ihr Programm diese und
andere Eingabebeispiele korrekt bearbeiten.
- Die Auswahl der Knoten erfolgt immer in der Reihenfolge,
in der die Knoten ``entdeckt'' wurden (ein Knoten wird entdeckt,
sobald sich sein Abstand von unendlich auf einen anderen Wert
ändert). Man muß also im ersten Teil der Aufgabe nicht unbedingt
in jedem Schritt alle Knoten nach einem noch nicht ausgewählten
mit kürzestem Abstand durchsuchen, sondern kann sich die
entdeckten aber noch nicht gewählten Knoten merken und in der
selben Reihenfolge bearbeiten (auswählen).
- Der bei der Entdeckung eines neuen Knotens gerade
ausgewählte Knoten ist ein zulässiger Vorgängerknoten auf dem
kürzesten Weg von 0 zum gerade entdeckten Knoten. Diese
Information kann im zweiten Teil bei der Rekonstruktion des Wegs
nützlich sein.
- Voraussichtlich werden wir die Suche nach einem kürzesten
Weg auf dem nächsten Blatt nochmals verwenden und dabei dieses
Programm erweitern.
Christian Ehrhardt
2006-11-28