INFORMATION
LETTER on the Dagstuhl Workshop
MODELLING OF COMMUNICATION NETWORKS VIA
STOCHASTIC GEOMETRY
held on March 25-28, 1998, at the International Conference Center
"Schloss Dagstuhl", in D-66687
Wadern, between Saarbrücken and Trier (Germany).
The aim of this workshop was to bring together a representative group
of
-
Applied probabilists and statisticians interested in the development of
new models based spatial point processes and stochastic geometry for modelling
communication networks;
-
Computer scientists and engineers working in the design of the architecture
of communication networks, particularly cellular communication systems;
-
Economists focusing on cost analysis and on production functions for large
communication networks.
The topics of interest included but were not limited to the following list:
-
basic stochastic geometry patterns for communication networks;
-
identification of stochastic models for spatial point patterns, line patterns,
etc. in this framework;
-
their statistical analysis and Monte Carlo simulation;
-
random tessellations (Voronoi tesselation, Delaunay triangulation, power
tesselations, etc.) and random coverage processes (Boolean model, germ-grain
model, etc.) for modelling wired and wireless communications;
-
problems of spatial interference and random resource management (measurement-based
power control, channel assignement, call access control, etc.) in cellular
radio communications
-
stochastic modelling of propagation and (hard/soft) hand-off in mobile
communications;
-
stochastic geometry representation of mobility;
-
modelling of architecture of large networks;
-
global cost analysis of communication networks; cost function of access,
traffic and transmission in communication networks.
ORGANIZERS
Professor
Francois Baccelli
INRIA Sophia Antipolis
2004, Route des Lucioles
B.P. 93
F-06902 Sophia Antipolis Cedex
baccelli@sophia.inria.fr |
Professor
Volker Schmidt
University of Ulm
Institute of Stochastics
Helmholtzstr. 18
D-89069 Ulm
schmidt@mathematik.uni-ulm.de |
PROGRAMME OF LECTURES
THURSDAY 03/26/1998
|
| INTRODUCTORY SESSION |
| 08:35-08:45 |
Opening |
|
| |
|
|
| 08:45-09:30 |
Daley, D. |
Introduction to Spatial Point Processes |
| |
|
|
| 09:30-10:15 |
Schmidt, V. |
Marked Point Processes and Tessellations in the Plane
|
| MOBILITY AND WIRELESS NETWORKS I |
| 10:30-11:15 |
Massey, W.A. |
The Poisson Arrival Location Model: a Stochastic
Offered Load Model for Space and
Time Dynamics in Wireless Communication Systems |
| |
|
|
| 11:15-11:45 |
Hanly, S. |
Traffic Modelling of Spatially Distributed Mobiles,
and Performance of CDMA |
| |
|
|
| 11:45-12:15 |
Zuyev, S. |
Evaluation and Optimization of Handover in Cellular
Communication Networks
|
| SPATIAL STATISTICS AND SIMULATION |
| 13:45-14:30 |
Baddeley, A. |
Nonparametric Analysis and Modelling of Spatial Point
Patterns |
| |
|
|
| 14:30-15:15 |
Isham, V. |
Point Process-Based Models for Spatio-Temporal Processes
|
| 15:30-16:15 |
Baccelli F. |
Poisson-Voronoi Spanning trees with Applications
to the Optimization of
Communication Networks Architecture |
| |
|
|
| 16:15-16:45 |
Gloaguen, C. |
Intersection of two Voronoi Tessellations with Applications
to Cost Analysis
|
| POINT PROCESSES AND TESSELLATIONS I |
| 17:15-17:45 |
Frey, A. |
Series Expansion for Characteristics of Boolean Models |
| |
|
|
| 17:45-18:15 |
Heinrich, L. |
Contact and Cord Length Distribution of a Stationary
Voronoi Tessellation
|
FRIDAY 03/27/1998
|
| MOBILITY AND WIRELESS NETWORKS II |
| 08:30-09:15 |
Mathar, R. |
Optimum Mirror-HLR Locations by a Markovian Mobility
Model |
| |
|
|
| 09:15-09:45 |
Hartmann, C. |
Modelling of User Distribution Mobility and Teletraffic
for SDMA System Simulations |
| |
|
|
| 09:45-10:15 |
Makowski, A.M. |
From Optimal Search Theory to Sequential Paging in
Cellular Networks
|
| SPATIAL QUEUES AND MARKOV MODELS I |
| 10:30-11:00 |
Daley, D. |
Erlang's Loss Formula when Customers have Different
Capacity Requirements |
| |
|
|
| 11:00-11:30 |
Jelenkovic, P. |
Packing Random Intervals On-Line |
| |
|
|
| 11:30-12:00 |
Serfozo, R.F. |
Spatial Queueing Systems
|
| 13:30-14:15 |
Lebourges, M. |
Stochatic Geometry Applied to Telecommunication Network
Cost Analysis:
Issues, Results and Open Problems |
| |
|
|
| 14:15-14:45 |
Le Madec, I. |
Traffic Production Functions |
| |
|
|
| 14:45-15:15 |
Mannersalo, P. |
Telecommunication Networks and Multifractal Analysis
of Human Population Distribution
|
| POINT PROCESSES AND TESSELLATIONS II |
| 15:30-16:15 |
Klein, M. |
Locally Stationary Processes and Palm Measures |
| |
|
|
| 16:15-16:45 |
Last, G. |
Stationary Flows and Palm Probabilities of Surface
Processes
|
| MOBILITY AND WIRELESS NETWORKS III |
| 17:15-17:45 |
Stolyar, A. |
Models of Uplink Interference in Cellular CDMA |
| |
|
|
| 17:45-18:15 |
Tchoumatchenko, K. |
Routing on the Delaunay Graph
|
SATURDAY 03/28/1998
|
| POINT PROCESSES AND TESSELLATIONS III |
| 08:30-09:15 |
Baum, D. |
On Some Markovian Spatial Processes |
| |
|
|
| 09:15-09:45 |
Remiche, M.-A. |
Asymptotic Poisson Distribution in Isotropic PH Planar
Point Processes |
| |
|
|
| 09:45-10:15 |
Zuyev, S. |
Variational Techniques for Point Processes with Applications
to Telecommunications
|
| MOBILITY AND WIRELESS NETWORKS IV |
| 10:30-11:00 |
Boucherie R. |
An Insensitive Queueing Network Model for Cellular
Mobile Communications Networks |
| |
|
|
| 11:00-11:30 |
Tutschku, K. |
Demand-Based Cellular Network Design Using Discrete
Point Patterns
|
| SPATIAL QUEUES AND MARKOV MODELS II |
| 11:45-12:15 |
Asmussen, S. |
Point Processes with Finite Dimensional Prediction
Processes |
| |
|
|
| 12:15-12:45 |
Breuer, L. |
Operator-Geometric Stationary Distributions for Spatial
Queues |
| |
|
|
| 12:45-13:15 |
Rolski, T. |
On a Poisson Hyperbolic Staircase
|
ABSTRACTS
POINT PROCESSES WITH FINITE DIMENSIONAL PREDICTION PROCESSES
ASMUSSEN, S.
LUND UNIVERSITY, SWEDEN
We study the structure of point processes N with the property that
conditioning on 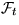 ,
the
,
the 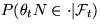 vary in a finite dimensional space of measures, where
vary in a finite dimensional space of measures, where 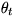 is the shift and
is the shift and 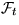 the
the 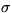 -field
generated by the counting process up to time t. Such a point process
is more general than the Markovian arrival process of Neuts (1979) (for
example, it allows for interarrival times which are matrix-exponential
but not phase-type), but we show that all analytic formulas for joint densities
of interarrival times, Palm distributions etc. have just the same form
in terms of two matrices C,D. We also give an explicit description
of the predicition process as a piecewiese deterministic Markov process
on a compact convex subset of Euclidean space.
-field
generated by the counting process up to time t. Such a point process
is more general than the Markovian arrival process of Neuts (1979) (for
example, it allows for interarrival times which are matrix-exponential
but not phase-type), but we show that all analytic formulas for joint densities
of interarrival times, Palm distributions etc. have just the same form
in terms of two matrices C,D. We also give an explicit description
of the predicition process as a piecewiese deterministic Markov process
on a compact convex subset of Euclidean space.
Joint work in progress with Mogens Bladt, IIMAS, National University
of Mexico.
POISSON-VORONOI SPANNING TREES
WITH APPLICATIONS TO THE OPTIMIZATION OF COMMUNICATION
NETWORKS
BACCELLI, F.
INRIA, SOPHIA ATIPOLIS, FRANCE
We define a family of random trees in the plane. Their nodes of level 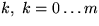 are the points of a homogeneous Poisson point process
are the points of a homogeneous Poisson point process 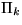 ,
whereas their arcs connect nodes of level k and k+1, according
to the least distance principle: if V denotes the Voronoi cell w.r.t.
,
whereas their arcs connect nodes of level k and k+1, according
to the least distance principle: if V denotes the Voronoi cell w.r.t. 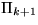 with nucleus x, where x is a point of
with nucleus x, where x is a point of 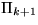 ,
then there is an arc connecting x to all the points of
,
then there is an arc connecting x to all the points of 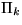 which belong to V. This creates a family of stationary random trees
rooted in the points of
which belong to V. This creates a family of stationary random trees
rooted in the points of 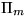 .
These random trees are useful to model the spatial organization of several
types of hierarchical communication networks. In relation with these communication
networks, it is natural to associate various cost functions with such random
trees. Using point process techniques, like the exchange formula between
two Palm measures, and integral geometry techniques, we show how to compute
these average costs in function of the intensity parameters of the Poisson
processes. The formulas which are derived for the average value of these
cost functions can then be exploited for parametric optimization purposes.
.
These random trees are useful to model the spatial organization of several
types of hierarchical communication networks. In relation with these communication
networks, it is natural to associate various cost functions with such random
trees. Using point process techniques, like the exchange formula between
two Palm measures, and integral geometry techniques, we show how to compute
these average costs in function of the intensity parameters of the Poisson
processes. The formulas which are derived for the average value of these
cost functions can then be exploited for parametric optimization purposes.
Joint work with S. Zuyev (INRIA, Sophia).
NONPARAMETRIC ANALYSIS AND MODELLING OF SPATIAL POINT PATTERNS
BADDELEY, A.
UNIVERSITY OF W. AUSTRALIA, NEDLANDS, AUSTRALIA
We review two approaches to the analysis of spatial point pattern data:
(1) exploratory data analysis using summary statistics such as the F,G
and K functions, (2) parametric or semi-parametric model fitting.
In approach (1), recent progress includes the development of another
summary function J, with good properties and some connections with survival
analysis. We describe the J function and some of its extensions.
As an example of progress in approach (2) we describe a technique for
computing approximate maximum pseudolikelihood estimates of the parameters
of a spatial point process. The method is an extension of Berman and Turner's
device for maximising the likelihoods of inhomogeneous spatial Poisson
processes. For a very wide class of spatial point process models, the likelihood
is intractable, while the pseudolikelihood is known explicitly, except
for the computation of an integral over the sampling region. Approximating
this integral by a finite sum yields an approximate pseudolikelihood which
is formally equivalent to the likelihood of a loglinear model with Poisson
responses. This can be maximised using standard statistical software for
generalised linear or additive models, provided the conditional intensity
of the process takes an `exponential family' form. Using this approach
we are able to rapidly fit a wide variety of spatial point process models
of Gibbs type, incorporating spatial trends, interaction between points,
dependence on spatial covariates, and mark information.
Joint work with T. Rolf Turner (New Brunswick).
ON SOME MARKOVIAN SPATIAL PROCESSES
BAUM, D.
UNIVERSITY OF TRIER, GERMANY
Spatial point processes have been increasingly over the last decade in
different areas as, for instance, image processing and pattern recognition,
statistical mechanics, and applied mathematics. Recently, the computer
science branch of telecommunications has recognized their applicability
and benefit for modelling the spread of active users over urban or rural
areas with its impact on performance in cellular mobile communcation systems.
In this paper the chronological evolution of (in case marked) spatial Poisson
point distributions, being controlled by some Markov random field, is investigated.
The structure of these processes is that of a spatial version of N-processes
(also BMAPs in the literature) and, as a consequence, can be described
in terms of a convolutional exponential distribution.
Keywords: Gibbs processes, Markov random fields, spacial BMAPs.
AN INSENSITIVE QUEUEING NETWORK MODEL FOR CELLULAR MOBILE COMMUNICATIONS
NETWORKS
BOUCHERIE, R.
UNIVERSITY OF AMSTERDAM, THE NETHERLANDS
We present a queueing network model for cellular mobile communications
networks. The model includes handovers, and generally distributed call
lengths. Under mild assumptions, the equilibrium distribution of the number
of calls in the cells of the network is shown to be of product form. Moreover,
this distribution depends on the call holding time distribution only through
its mean. The result enables performance analysis (e.g. computation of
call blocking probabilities) based on easily measurable characteristics
of the cellular network.
OPERATOR-GEOMETRIC STATIONARY DISTRIBUTIONS FOR SPATIAL QUEUES
BREUER, L.
UNIVERSITY OF TRIER, GERMANY
The following queue will be discussed. Users appear with interarrival time
distribution H (iid) in an area. The position they appear at is distributed
(iid) abiding by a distribution on 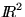 ,
which will be denoted by
,
which will be denoted by 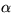 .
.
Service times are distributed exponentially with rate c depending
on the position of the user served. A single server moves from one user
to the other. After serving one, the next user it moves to is determined
by a function 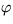 of the positions of all other waiting users and the server's position.
The time needed to move from one user to the next will be neglected.
of the positions of all other waiting users and the server's position.
The time needed to move from one user to the next will be neglected.
The model in E. Çinlar [1], section 4.5 ``Spatial M/M/1 queues''
coincides with the special case of exponential interarrival time distribution.
In the sequel, a closer determination of the stationary distribution shall
be undertaken.
Literature
[1] Çinlar, E.: An introduction to spatial queues. In:
J.H. Dshalalow (Ed.): ``Advances in Queueing'', CRC Press 1995.
INTRODUCTION TO SPATIAL POINT PROCESSES
DALEY, D.
AUSTRALIAN NATIONAL UNIVERSITY, CANBERRA, AUSTRALIA
The talk reviews ideas and constructs for spatial point patterns (e.g.
the book of Diggle), and for `spatio-temporal' point processes, meaning,
a spatial point pattern that evolves in time. We concentrate on basic notions
and terminology, partly because results are scarce and partly too because
possible uses of models of spatial point processes include performance
evaluation on the one hand, and parameter description for analysis on the
other.
ERLANG'S LOSS FORMULA WHEN CUSTOMERS HAVE DIFFERENT CAPACITY
REQUIREMENTS
DALEY, D.
AUSTRALIAN NATIONAL UNIVERSITY, CANBERRA, AUSTRALIA
The paper describes a situation, which can be motivated by spatial distribution
of customers, in which customers requiring service from a facility require
different intensity of service (e.g. through differential gain requirements)
from the service facility. Assuming the service facility has finite capacity,
the number of customers that can be accommodated at any time is constrained
by the total intensity of the customers in service. The probability of
lost calls (i.e. of prospective customers being refused connection) can
be found via a formula reminiscent of Erlang's loss formula. Proof of the
formula is simply motivated, and also relates to reversibility properties.
SERIES EXPANSION FOR CHARACTERISTICS OF BOOLEAN MODELS
FREY, A.
UNIVERSITY OF ULM, GERMANY
A general concept is considered of expanding the expectation of a wide
class of functionals of marked point processes in d-dimensional
Euclidean space. This expectation is approximated by a sum of integrals
over higher-order factorial moment measures of the underlying point process
[2]. In the Poisson case one can show that, under some additional assumptions
on the considered class of functionals, a Taylor series expansion with
respect to the intensity of the Poisson process is obtained, see [1].
The idea of factorial moment expansion is applied in order to derive
approximation formulas for characteristics of Boolean models. For example
we consider the two-dimensional Boolean model which grains are circles
with random radius and which can be used to model the power of users (germs)
in a mobile communication system [3]. The intersection with a line (road)
form a one-dimensional Boolean model, where the clumps of intersection
segments can be interpreted as the regions of interference on the road.
Hence one is intereseted in the covered and uncovered parts of the road.
For the distribution of the length L of a typical clump, we derive
an approximation formula of the form 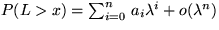 ,where
,where 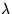 is the intensity of the underlying Poisson process, and we give a recursion
formula for the coefficients ai. Furthermore, we derive
an approximation of the same kind for the distribution of the sum V
of the uncovered parts in a given interval.
is the intensity of the underlying Poisson process, and we give a recursion
formula for the coefficients ai. Furthermore, we derive
an approximation of the same kind for the distribution of the sum V
of the uncovered parts in a given interval.
For the expected clump length of the two-dimensional Boolean model,
which grains are segments with random length and orientation, similar approximation
formulas can be derived [4].
Numerical experiments demonstrate the goodness of the approximations.
Literature
[1] F. Baccelli, S. Hasenfuss and V. Schmidt (1997) Differentiability
of functionals of Poisson processes via coupling. Preprint, INRIA Sophia
Antipolis/University of Ulm.
[2] B. B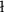 aszczyszyn,
E. Merzbach and V. Schmidt (1997) A note on expansion for functionals
of spatial marked point processes. Statistics and Probability Letters
36, 299-306.
aszczyszyn,
E. Merzbach and V. Schmidt (1997) A note on expansion for functionals
of spatial marked point processes. Statistics and Probability Letters
36, 299-306.
[3] A. Frey and V. Schmidt (1997) Marked point processes in the
plane I - a survey with applications to spatial modeling of communication
networks. Advances in Performance Analysis (to appear).
[4] C. Rau (1997) Series expansion for characteristics of Boolean
models. Diploma thesis, University of Ulm.
INTERSECTION OF TWO VORONOI TESSELLATIONS
GLOAGUEN, C.
FRANCE TELECOM, PARIS, FRANCE
Let T1 and T2 be the Voronoi tessellations generated by two stationary
point processes N1 and N2 in the plane. This paper focuses on the compound
tessellation T, the cells of which are intersections of cells of T1 and
T2.
To each cell of T, one can associate its center of gravity. This defines
a new stationary point process Z. The cells of T are of different types
depending on whether they contain both a point of N1 and a point of N2,
only one of them, or none of them. These types define various stationary
sub-processes of Z. A few basic geometrical characteristics of these cells
are considered using Palm probabilities with respect to Z and its sub-processes.
The particular case where N1 and N2 are independent Poisson processes
is studied in detail. Using the mean characteristics relationship for planar
tessellations, we obtain explicit expressions for the geometrical characteristics
of a typical cell under the Palm probability with respect to Z. Integral
representations are also derived for the mean value of the area of the
cell which contains the origin, under other probability measures, including
the Palm probability with respect to the sub-processes of Z, and the underlying
stationary probability measure. Asymptotic expansions in k, the ratio of
the intensities of the two processes, are used to evaluate these integrals.
Such compound tessellations arise naturally when considering the interconnection
of subscribers of two competing telecommunication operators. Here, the
point processes N1 and N2 represent the locations of the concentrators
of the two operators, whereas T1 and T2 represent the local zones associated
with these concentrators. Two subscribers, one of operator 1, and the other
of operator 2, belonging to the same cell of T induce different interconnection
costs depending on the type of the cell they belong to.
TRAFFIC MODELLING OF SPATIALLY DISTRIBUTED MOBILES, AND PERFORMANCE
OF CDMA
HANLY, S.
MELBOURNE UNIVERSITY, AUSTRALIA
We will consider two approaches to deal with modelling and performance
analysis for CDMA wireless networks. Both focus on the space varying nature
of the network, and in the first approach dynamic time-variation is also
considered.
In the first approach, we assume mobiles move independently, but interact
through the mutual interference they create for each other. Users control
their transmitter powers to counteract their own path losses, but do not
react to the power levels of other users. We show that if the arrival process
of calls is Poisson, then at any instant the spatial distribution of traffic
is Poisson, and using Campbell's theorem we can calculate the mean and
variance of other-cell interference. Using the fact in-cell interference
is Poisson, and taking a Gaussian approximation for the other-cell interference,
we show how outage probabilities can be calculated. This approach requires
the spatial traffic intensity function to be known over time, perhaps by
direct measurement.
In the second approach, we allow the power levels of users to interact.
This is more efficient from a signal processing point of view, but makes
performance analysis much harder. In this part of the talk we do not consider
time-variation, but that is definitely in the background. For simplicity,
we consider how to measure spatial congestion for a given fixed set of
users distributed in space. We use a matrix description of the network
configuration, and show how the Perron-Frobenius eigenvalue measures congestion,
whether that be due to a localized hotspot, or to network-wide congestion.
MODELLING OF USER-DISTRIBUTION, MOBILITY AND TELETRAFFIC FOR
SDMA-SYSTEM SIMULATIONS
HARTMANN, C.
TECHNICAL UNIVERSITY OF MUENCHEN, GERMANY
A promising technique to enhance the spectral efficiency of future mobile
communication systems is the exploitation of the space domain using smart
antennas. The deployment of adaptive anntenna arrays will enable base stations
to form directional beam patterns, separating signals arriving from different
directions on the uplink and providing single mobiles with sufficient power
while minimizing the radiated power in unwanted directions on the downlink.
Thus, it becomes possible to serve multiple users within a cell on the
same channel, where a channel can be a speciffic frequency, timeslot or
code, depending on the underlying multiple access scheme (F/T/CDMA). This
reuse of channels within a cell is called SDMA (Space Division Multiple
Access) and adds a spatial component to the access scheme. The additional
gain in capacity through SDMA depends on the number of users which can
simultaneously operate on the same channel. From the antenna array point
of view, users operating on the same channel must be sufficiently separable
in the space domain. Thus, the spatial distribution of currently active
users is crutial for the number of users that can be served at the same
time. Therefore, in order to predict capacity gains of SDMA-Systems, the
mobile users behaviour, which determines the positions of the currently
active users at each time instant, has to be taken into account. The relevant
aspects of the users behaviour are the spatial distribution, the mobility
and the generated traffic. Since realistic models of above aspects yield
a complexity which is virtually impossible to be handled in a pure analytic
way, simulation appears to be an appropriate alternative. Thus, in this
presentation a set of models for the user distribution, mobility and teletraffic
is proposed as well as a concept to apply those models to montecarlo simulations
of SDMA-Systems. Using the proposed concept, various scenarios can be modeled
in order to compare the achievable gain in spectral capacity of SDMA-Systems
with respect to different scenarios. Some results of simulations, focussing
on the impact of inhomogeneous user distribution on call blocking probabilities,
conclude the presentation.
CONTACT AND CHORD LENGTH DISTRIBUTION OF A STATIONARY VORONOI
TESSELLATION
HEINRICH, L.
UNIVERSITY OF AUGSBURG, GERMANY
We derive a formula of comparatively simple structure for the contact distribution
function of a stationary Voronoi tessellation w.r.t. any compact, star-shaped
`structuring element' containing the origin. Based on a well-known relationship
between the linear contact distribution and the chord length distribution
we can express the chord length distribution function in terms of a two-point
Palm void probability of the generating point process. In particular a
closed - term expression for the mean chord length is given which in case
of a stationary Poisson-Voronoi tessellation reproves Gilbert's 1962 formula.
Our general formulae are discussed for several classes of non-Poisson-
Voronoi-tessellations. In case of an underlying stationary Gibbsian point
process with parametrized pair potential the obtained formula of the contact
distribution functions seems to be useful to estimate the involved parameters
via the Takacs-Fiksel procedure.
POINT PROCESS-BASED MODELS FOR SPATIO-TEMPORAL PROCESSES
ISHAM, V.
UNIVERSITY COLLEGE LONDON, ENGLAND
A role for multidimensional point processes in modelling continuous spatial
processes, and their temporal evolution, will be described. A particular
application involving a stochastic spatio-temporal model of precipitation
developed to address problems in hydrology will be introduced. The fitting
and assessment of the adequacy of fit of such models raise many interesting
statistical and computational issues, some of which will be discussed briefly.
PACKING RANDOM INTERVALS ON-LINE
JELENKOVIC, C.
BELL LABORATORIES, MURRAY HILL, USA
Starting at time 0, unit-length intervals arrive and are placed on the
positive real line by a unit-intensity Poisson process in two dimensions;
the probability of an interval arriving in the time interval ![$[t,t+\Delta t]$](img18.gif) with its left endpoint in
with its left endpoint in ![$[y,y+\Delta y]$](img19.gif) is
is 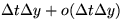 .
Fix
.
Fix 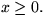 An arriving interval is accepted if and only if it is contained
in [0,x] and overlaps no interval already accepted.
An arriving interval is accepted if and only if it is contained
in [0,x] and overlaps no interval already accepted.
We study the number Nx(t) of intervals accepted
during [0,t]. By Laplace-transform methods, we derive large-x
estimates of 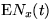 and
and 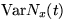 with error terms exponentially small in x uniformly in
with error terms exponentially small in x uniformly in 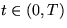 ,
where T is any fixed positive constant. We prove that, as
,
where T is any fixed positive constant. We prove that, as 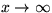 ,
, 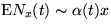 ,
, 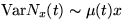 ,uniformly
in
,uniformly
in 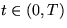 ,where
,where 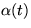 and
and 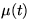 are given by explicit, albeit complicated formulas. Using these asymptotic
estimates we show that Nx(t) satisfies a central
limit theorem, i.e., for any fixed t
are given by explicit, albeit complicated formulas. Using these asymptotic
estimates we show that Nx(t) satisfies a central
limit theorem, i.e., for any fixed t
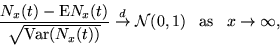 where
where 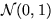 is a standard normal random variable, and
is a standard normal random variable, and 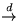 denotes convergence in distribution. This stochastic, on-line interval
packing problem generalizes the classical parking problem, the latter corresponding
only to the absorbing states of the interval packing process, where successive
packed intervals are separated by gaps less than 1 in length. We verify
that, as
denotes convergence in distribution. This stochastic, on-line interval
packing problem generalizes the classical parking problem, the latter corresponding
only to the absorbing states of the interval packing process, where successive
packed intervals are separated by gaps less than 1 in length. We verify
that, as 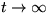 ,
,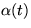 and
and 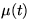 converge to
converge to 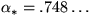 and
and 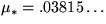 ,
the constants of Renyi and Mackenzie for the parking problem. Thus, by
comparison with the parking analysis in a single space variable, ours is
a transient analysis involving both a time and space variable.
,
the constants of Renyi and Mackenzie for the parking problem. Thus, by
comparison with the parking analysis in a single space variable, ours is
a transient analysis involving both a time and space variable.
Our interval packing problem has applications similar to those of the
parking problem in the physical sciences, but the primary source of our
interest is the modeling of reservation systems, especially those designed
for multi-media communication systems to handle high-bandwidth, real-time
demands.
Joint work with E.G. Coffman Jr, L. Flatto (Bell Labs) and B. Poonen
(University of California).
LOCALLY STATIONARY PROCESSES AND PALM MEASURES
KLEIN, M.
FRANCE TELECOM-CNET, ISSY LES MOULINEAUX, FRANCE
Spatial modeling of telecommunication networks requires the introduction
of finite point processes. Local invariance under the action of a group
(rotations, translations) is also needed. We propose in this talk a generalization
of the classical theory of stationary processes. Our processes are defined
on any open sub-set of a topological group and from the local definition
of Haar measure we deduce a local Palm measure.
STATIONARY FLOWS AND PALM PROBABILITIES OF SURFACE PROCESSES
LAST, G.
TECHNICAL UNIVERSITY OF BRAUNSCHWEIG, GERMANNY
We consider a random surface 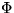 tesselating the space into cells and a random vector field u which
is smooth on each cell but may jump on the boundaries. Assuming the pair
tesselating the space into cells and a random vector field u which
is smooth on each cell but may jump on the boundaries. Assuming the pair 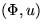 stationary, we present an inversion formula expressing the stationary probability
measure in terms of the Palm probability
stationary, we present an inversion formula expressing the stationary probability
measure in terms of the Palm probability 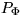 defined by the random surface associated with
defined by the random surface associated with 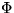 .
As an application we derive necessary and sufficient conditions for the
flow of u to be volume preserving. A second application deals with
the spherical contact distribution of germ-grain models.
.
As an application we derive necessary and sufficient conditions for the
flow of u to be volume preserving. A second application deals with
the spherical contact distribution of germ-grain models.
Joint work with R. Schassberger (Technical University of Braunschweig).
ASYMPTOTIC POISSON DISTRIBUTION IN ISOTROPIC PH PLANAR POINT
PROCESSES
REMICHE, M.-A.
UNIVERSITE LIBRE DE BRUXELLES, BELGIUM
We consider a family of planar point processes which are a natural generalization
of the two-dimensional Poisson process. In this family, points are located
on a sequence of concentric circles centered at the origin; the radius
of the circles are chosen through a phase-type construction. These processes
are called Ph Planar Point Processes. Although point patterns obtained
in this fashion are very different from those of the Poisson process, nevertheless
we show that if one considers the region of the plane far away from the
origin, the Ph process exhibit some similarities to the Poisson process.
Joint work with G. Latouche (Université Libre de Bruxelles).
STOCHASTIC GEOMETRY APPLIED TO TELECOMMUNICATION NETWORKS COST
ANALYSIS :
ISSUES, RESULTS AND OPEN PROBLEMS
LEBOURGES, M.
FRANCE TELECOM, PARIS, FRANCE
Stochastic geometry is a new approach to address telecommunication network
cost analysis. It is intended to lead to explicit analytical relations
between synthetic variables describing the demand offered to a telecommunications
network, the architecture of this network, and the characteristics of the
network cost. Such synthetic relations are directly relevant for commercial,
regulatory and technological decision making in the telecommunications
business.
To which extend do existing stochastic geometry models and results meet
this end, and what future work would improve the applicability of the theory
to actual telecommunication problems ?
Telecommunications network are technically complex and models integrating
full deterministic descriptions of a network are incompatible with the
synthetic economical analysis tools needed by the telecommunication industry.
Existing stochastic geometry models are shown to be robust and reliable
and can already be used in economical analysis. However, they cover only
a small part of problems to be addressed. So new stochastic geometry research
is needed, in mathematics and in statistics, both to improve existing models
and to cover new fields.
TRAFFIC PRODUCTION FUNCTIONS
LE MADEC, I.
FRANCE TELECOM-CNET, DAC/GTR, ISSY LES MOULINEAUX,
FRANCE
The paper presents an analytical expression for traffic production functions.
It is based on a probabilistic study in which a network model relies on
stochastic geometry concepts. For a full description of networks, a macroscopic
model reduces the relevant amount of data to a few meaningful parameters.
This model aims to be relatively realistic. When completed, it should be
a source of interesting statistics on transmission and commutation needs
which are a basis for cost evaluations.
The network architecture, which is described first, basically consists
of a hierarchy of switched sub-networks, a connection architecture between
the switches on the different levels according to traffic hypothesis on
the links. A cost formula is then defined as a set of relations between
relevant network parameters. Finally, a global cost formula is established.
Joint work with C. Gloaguen (France Telecom-Cnet DAC/GTR) and M. Lebourges
(France Telecom-Cnet DPS/SEE, Paris).
FROM OPTIMAL SEARCH THEORY TO SEQUENTIAL PAGING IN CELLULAR
NETWORKS
MAKOWSKI, A.
UNIVERSITY OF MARYLAND, USA
We review issues of paging in cellular networks, and propose a novel paging
strategy based on the theory of optimal search with discrete effort. When
compared to conventional paging methods, the proposed scheme increases
the mobile station discovery rate while decreasing the average number of
times that a mobile station has to be paged in a location area. The proposal
is fully compatible with existing cellular structure and requires minimal
computational power in the mobile switching centers.
TELECOMMUNICATION NETWORKS AND MULTIFRACTAL ANALYSIS OF HUMAN
POPULATION DISTRIBUTION
MANNERSALO, P.
VTT INFORMATION TECHNOLOGY, ESPOO, FINLAND
S. Appleby has recently applied multifractal analysis of population distribution
to cost analysis of large telecommunication networks. Using his approach
and accurate Finnish population data, we show that the population distribution
of Finland exhibits multifractal scaling over a large range of resolutions.
A relation between generalized q-dimensions and minimal cable length needed
to interconnect the whole population by N star networks is demonstrated.
Furthermore, a cost estimate suitable for dimensioning hierarchical networks
is presented.
Joint work with A. Koski and I. Norros (VTT Information Technology).
THE POISSON ARRIVAL LOCATION MODEL: A STOCHASTIC OFFERED LOAD
MODEL FOR SPACE AND TIME DYNAMICS IN WIRELESS COMMUNICATION SYSTEMS
MASSEY, W.A.
BELL LABORATORIES, MURRAY HILL, USA
In C. Palm's classic 1943 paper, he recognized the importance of queueing
models with time-dependent arrival rates and proposed using the infinite-server
queueing system both as a model of the offered load traffic and as a means
to study the corresponding loss model. We extend this approach by developing
the Poisson-arrival-location-model (PALM), in which arrivals generated
by a nonhomogeneous Poisson process move independently through a general
state space according to a location stochastic process that is not necessarily
Markovian. PALM is a generalization of infinite server networks and it
precisely the offered load model for a mobile wireless communication system.
We will also describe a special PALM for communicating mobiles on a highway
and define key processes which are related by fundamental conservation
equations.
This is based on joint work with both Ward Whitt and Kin Leung (AT&T
Labs Research).
OPTIMUM MIRROR-HLR LOCATIONS BY A MARKOVIAN MOBILITY MODEL
MATHAR, R.
AACHEN UNIVERSITY OF TECHNOLOGY, GERMANY
As a new policy, Mirror Home Location Registers (MHLR) are introduced to
avoid expensive signalling traffic of roaming users to a far distant HLR
in mobile communication networks. We investigate the question what the
optimum location strategy will be. Three basic ingredients are necessary
to tackle this problem:
-
1.
-
A realistic, but tractable, mobility model,
-
2.
-
a precise description of signalling costs, and
-
3.
-
an optimization method to solve the complicated minimization problems.
This paper contributes to each of these points in the following way:
-
1.
-
An open Jackson network with customer classes is developed to describe
user mobility and network flows.
-
2.
-
A careful analysis of the number of signalling messages and database accesses
yields an accurate cost function.
-
3.
-
In steady state of the network, integer linear programming is used to find
an optimal register allocation strategy for the so called dedicated MHLR
policy, where each location area is assigned to an individual MHLR.
Numerical examples show that the optimum Mirror HLR strategy clearly outperforms
the previously suggested Local Anchoring scheme and standard GSM signalling
protocols.
Joint work with M. Hellebrandt (Aachen University of Technology).
ON A POISSON HYPERBOLIC STAIRCASE
ROLSKI, T.
UNIVERSITY OF WROCLAW, POLAND
In the talk a class of zigzag processes defined on a planar Poisson process
is considered. In particular we study the Poisson hyperbolic staircase 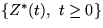 ,
which is a decreasing sstep process with several remarkable properties.
,
which is a decreasing sstep process with several remarkable properties.
-
1.
-
The process is Markovian, with finite dimensional distributions which are
multivariate exponential in the sense of Marshall-Olkin, in particular
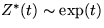 and hence E(Z*(t))=1/t,
and hence E(Z*(t))=1/t,
-
2.
-
The counting process of the jumps is a non-homogeneous Poisson process
with rate 1/t.
-
3.
-
The process fulfills the distributional equation that
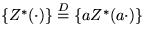 ,
where a>0. Notice that functional equation f(x)= a
f(ax) has the solution f(x)=f(1)/x
and hence the name hyperbolic.
,
where a>0. Notice that functional equation f(x)= a
f(ax) has the solution f(x)=f(1)/x
and hence the name hyperbolic.
-
4.
-
The process
 is symmetric around the line x=t: The inverse process
is symmetric around the line x=t: The inverse process 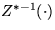 defined by
defined by 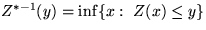 is
equal in distribution to
is
equal in distribution to 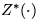 .
.
Joint work with Benny Levikson and Gideon Weiss (University of Haifa).
MARKED POINT PROCESSES AND TESSELATIONS IN THE PLANE
SCHMIDT, V.
UNIVERSITY OF ULM, GERMANY
The talk gives an introduction to stochastic models for planar point patterns
which can be applied to investigate the spatial organization of large comunication
networks. We focus on stationary marked point processes, where the stationary
Poisson process provides a basic reference model against which to compare
other models where effects of clustering or regularity of points are incorporated.
Particular emphasis will be put on some fundamental properties of random
tessellations and of the Boolean model induced by a stationary Poisson
process. We also mention some elementary statistical methods interrelating
the models with empirical data, as well as some simulation methods to generate
samples of planar point patterns.
Joint work with Andreas Frey (University of Ulm).
SPATIAL QUEUEING SYSTEMS
SERFOZO, R.
GEORGIA INSTITUTE OF TECHNOLOGY, ATLANTA, USA
Queueing networks such as Jackson networks model movements of units (jobs,
customers etc.) among a finite set of nodes where the units are processed.
I will describe a class of "spatial queueing processes" for modeling systems
in which units move in a region or general set rather than a discrete network.
These are measure-valued Markov processes. Typical applications are cellular
phones, storage facilities, logistics systems and network with many nodes.
Spatial queueing processes also represent networks that contain non-discrete
quantities (e.g., oil, chemicals, gas, stress, resources for services)
that change over time. The talk will focus on characterizing stationary
distributions for these processes, which yield information on throughput
rates, customer delays and total processing times.
MODELS OF UPLINK INTERFERENCE IN CELLULAR CDMA
STOLYAR, A.
MOTOROLA, ARLINGTON HEIGHTS, USA
In the first one, both mobiles and base stations are distributed according
to a homogeneous Poisson process on the plane. The propagation loss model
is the "power law times a lognormal component". Each mobile is "controlled"
by the best (lowest propagation loss) of the N closest base stations. We
derive closed form expressions for the average interference level at a
base station in cases N=1, 2, and infinity. In the most important case,
N=infinity, the average interference is insensitive to the lognormal component
of the propagation loss.
In the second model, base station locations are arbitrary and mobile
density is arbitrary. We consider the power control problem for a deterministic
"fluid limit" of the system, and solve it through an efficient numerical
procedure. Comparison to simulation shows that the fluid limit system gives
good approximation for the average interference levels at the base stations.
ROUTING ON THE DELAUNAY GRAPH
TCHOUMATCHENKO, K.
INRIA, SOPHIA ANTIPOLIS, FRANCE
Consider the Delaunay graph and the Voronoi tessellation associated with
a Poisson point process. We define and analyze several paths of this graph,
allowing one to connect two of its vertices a and b, and
study their asymptotic properties when the distance between a and
b grows. A first path of interest is the shortest one. The existence
of a linear asymptotic length follows from subadditive ergodic theory.
A second path of interest is defined from the line between a and
b. The sequence of nuclei of the Voronoi cells crossed by this line
constitutes the set of vertices of the path. We show that the segments
of this path form a Markov chain. We study the mean drift behavior of this
chain, prove several stability results, and find its stationary distribution.
As a corollary, we obtain the ratio relating the path length and the Euclidean
distance between the end points. A third path is defined recursively as
follows: if the n-th cell nucleus of the path is z, the n+1-st
is the nucleus of the neighboring cell which is the closest of a.
We show how these paths can be used to define simple routing algorithms
in packet communications networks with guaranteed mean or asymptotic performance.
DEMAND-BASED CELLULAR NETWORK DESIGN USING DISCRETE POINT PATTERNS
TUTSCHKU, K.
UNIVERSITY OF WUERZBURG, GERMANY
In this presentation we introduce a demand-based engineering method for
designing radio networks of cellular mobile communication systems using
discrete point patterns. The proposed procedure is based on a new forward-engineering
method, the "Integrated Approach" to cellular network planning. The new
approach is facilitated by the application of a discrete point population
model, denoted as the "Demand Node Concept". We show how the Demand Node
pattern can be derived from a geographical traffic model that uses public
available geographical and demographical data. The application of the Demand
Node Concept enables the formulation of the transmitter locating task as
a "Maximal Coverage Location Problem (MCLP)", which is well known in economics
for modeling and solving facility location problems. For the network optimization
task, we introduced the "Set Cover Base Station Positioning Algorithm (SCBPA)",
which is based on a greedy heuristic for solving the MCLP problem. Furthermore,
we present the planning tool prototype ICEPT (Integrated Cellular network
Planning Tool), which is based on these ideas and show a first result from
a real world planning case.
EVALUATION AND OPTIMIZATION OF HANDOVER IN CELLULAR COMMUNICATION
NETWORKS
ZUYEV, S.
INRIA, SOPHIA ANTIPOLIS, FRANCE
We construct a class of models based on random tessellations and Poisson
line processes allowing one to describe the phenomenon of hand-over in
cellular wireless communication networks. The closed form formulas obtained
in this framework enable us to determine the architecture which offers
the best trade-off between the search cost of mobiles and the paging cost
induced by mobility.
Joint work with F. Baccelli (INRIA, Sophia).
VARIATIONAL TECHNIQUES FOR POINT PROCESSES WITH APPLICATIONS
TO TELECOMMUNICATIONS
ZUYEV, S.
INRIA, SOPHIA ANTIPOLIS, FRANCE
We describe a variational technique for functionals of Poisson processes
and show its potential use for establishing the optimal distribution of
stations in a large telecommmunications network. The expression for the
stochastic gradient obtained in this framework leads to steepest descent
type algorithms which are implemented in a prototype of network topology
simulator.
Joint work with I. Molchanov (University of Glasgow).
LIST OF PARTICIPANTS
| Attahiru |
ALFA |
Dept. of Mechanical & Industrial Engineering |
| |
|
University of Manitoba |
| |
|
Winnipeg, Manitoba |
| |
|
Canada R3T 5V6 |
| |
|
Tel: +1 (204) 474-9173 |
| |
|
Fax: +1 (204) 275-7507 |
| |
|
email: alfa@cc.umanitoba.ca |
| |
|
|
| Soeren |
ASMUSSEN |
Department of Mathematical Statistics |
| |
|
Lund University |
| |
|
Box 118, |
| |
|
S-221 00 Lund |
| |
|
Sweden |
| |
|
Tel: +46 46 222 4747 |
| |
|
Fax: +46 46 222 4623 |
| |
|
email: asmus@maths.lth.se |
| |
|
|
| Francois |
BACCELLI |
INRIA |
| |
|
2004, Route des Lucioles |
| |
|
BP 93 |
| |
|
F-06902 Sophia Antipolis |
| |
|
France |
| |
|
Tel: +33 4 92 38 77 99 |
| |
|
Fax: +33 4 92 28 79 71 |
| |
|
email: bacceli@sophia.inria.fr |
| |
|
|
| Adrian |
BADDELEY |
Department of Mathematics |
| |
|
University of Western Australia |
| |
|
Nedlands (Perth) WA 6907 |
| |
|
Australia |
| |
|
Tel: +61 8 9380 3342 |
| |
|
Fax: +61 8 9380 1028 |
| |
|
email: adrian@maths.uwa.edu.au |
| |
|
|
| Dieter |
BAUM |
University of Trier |
| |
|
Dept. IV, Subdept. of Computer Science |
| |
|
D-54286 Trier |
| |
|
Germany |
| |
|
Tel: +49-651-201-2849/2848 |
| |
|
Fax: +49-651-201-3805 |
| |
|
email: baum@uni-trier.de |
| |
|
|
| Richard |
BOUCHERIE |
Universiteit van Amsterdam |
| |
|
Dept of Operations Research |
| |
|
Roetersstraat 11 |
| |
|
NL-1018 WB Amsterdam |
| |
|
Netherlands |
| |
|
Tel: +31 20 5254220 |
| |
|
email: boucheri@fee.uva.nl |
| |
|
|
| Lothar |
BREUER |
University of Trier |
| |
|
Dept. IV, Subdept. of Computer Science |
| |
|
D-54286 Trier |
| |
|
Germany |
| |
|
Tel: +49 651 201 2812 |
| |
|
Fax: 49 651 201 3805 |
| |
|
email: breuer@info04.uni-trier.de |
| |
|
|
| Patrice |
COUPE |
France Telecom-CNET |
| |
|
DAC/ORA |
| |
|
38-40, Rue du General Leclerc |
| |
|
F-92794 Issy Moulineaux |
| |
|
France |
| |
|
Tel: +33 1 45 29 52 97 |
| |
|
Fax: +33 1 45 29 60 69 |
| |
|
email: patrice.coupe@cnet.francetelecom.fr |
| |
|
|
| Hans |
DADUNA |
University of Hamburg |
| |
|
Institute of Mathematical Stochastics |
| |
|
Bundesstrasse 55 |
| |
|
D-20146 Hamburg |
| |
|
Germany |
| |
|
Tel: 040/ 4123-4930 |
| |
|
email: daduna@math.uni-hamburg.de |
| |
|
|
| Daryl |
DALEY |
School of Mathematical Sciences |
| |
|
Australian National University |
| |
|
Canberra ACT 0200 |
| |
|
Australia |
| |
|
email: daryl@orac.anu.edu.au |
| |
|
|
| Xavier |
DELACHE |
Autorite de Reglementation |
| |
|
des Telecommunications |
| |
|
20, av. de Segur |
| |
|
F-75007 Paris |
| |
|
France |
| |
|
Tel: +33 1 43 19 67 25 |
| |
|
Fax: +33 1 43 19 64 19 |
| |
|
|
| Elisabeth |
DOGNIN |
France Telecom (DRE/DRNE, Grenelle) |
| |
|
6 place d'Alleray |
| |
|
F-75505 Paris Cedex 15 |
| |
|
France |
| |
|
Tel: +33 1 44 44 01 23 |
| |
|
email: elisabeth.dognin@francetelecom.fr |
| |
|
|
| David |
EVERITT |
University of Melbourne |
| |
|
Dept. of Electrical and |
| |
|
Electronic Engineering |
| |
|
Grattan Street |
| |
|
Parkville, Victoria 3052 |
| |
|
Australia |
| |
|
email: d.everitt@ee.mu.oz.au |
| |
|
|
| Andreas |
FREY |
University of Ulm |
| |
|
Institute of Stochastics |
| |
|
D-89069 Ulm |
| |
|
Germany |
| |
|
Tel: +49 731 502 3527 |
| |
|
Fax: +49 731 502 3649 |
| |
|
email: frey@mathematik.uni-ulm.de |
| |
|
|
| Jerome |
GALTIER |
INRIA |
| |
|
2004, route des Lucioles |
| |
|
BP 93 |
| |
|
F-06902 Sophia Antipolis |
| |
|
France |
| |
|
Tel: +33 4 92 38 79 88 |
| |
|
Fax: +33 4 92 38 79 71 |
| |
|
email: Jerome.Galtier@sophia.inria.fr |
| |
|
|
| Catherine |
GLOAGUEN |
France Telecom/CNET/DAC/GTR |
| |
|
38-40 rue du General Leclerc |
| |
|
F-92794 Issy-Moulineaux Cedex 9 |
| |
|
France |
| |
|
Tel : +33 01 45 29 64 41 |
| |
|
Fax : +33 01 45 29 65 56 |
| |
|
email: gloaguen@issy.cnet.fr |
| |
|
|
| Francois Xavier |
GODRON |
France Telecom |
| |
|
DPS/SEE B 16 |
| |
|
6 Place d'Alleray |
| |
|
Annexe Brancion |
| |
|
F-75505 Paris Cedex 15 |
| |
|
France |
| |
|
Tel: +33 1-44-44-09-39 |
| |
|
Fax: +33 1-44-44-98-78 |
| |
|
email: francoisxavier.godron@francetelecom.fr |
| |
|
|
| Uwe |
GOTZNER |
E-Plus Mobilfunk GmbH |
| |
|
Abt. Funknetzplanung |
| |
|
E-Plus-Platz 1 |
| |
|
D-40468 Duesseldorf |
| |
|
Germany |
| |
|
Tel: 0211/448-4820 |
| |
|
Fax: 0211/448-4096 |
| |
|
email: ugotzner@eplus.de or |
| |
|
uwe.gotzner@eplus.de |
| |
|
|
| Stephen |
HANLY |
Dept. of Electrical Engineering |
| |
|
University of Melbourne |
| |
|
221 Bouverie St. |
| |
|
Carlton 3053 Vic. |
| |
|
Australia |
| |
|
Tel: +61 3 9344 9210 |
| |
|
Fax: +61 3 9344 9188 |
| |
|
email: s.hanly@ee.mu.oz.au |
| |
|
|
| Christian |
HARTMANN |
Technical University of Muenchen |
| |
|
Institute of Communication Networks (LKN) |
| |
|
Arcisstr. 21 |
| |
|
D-80290 Muenchen |
| |
|
Germany |
| |
|
Tel: +49 89 289-23509 |
| |
|
Fax: +49 89 289-23523 |
| |
|
email: hartmann@lkn.e-technik.tu-muenchen.de |
| |
|
|
| Lothar |
HEINRICH |
University of Augsburg |
| |
|
Institute of Mathematics |
| |
|
Universitaetsstr. 14 |
| |
|
D-86135 Augsburg |
| |
|
Germany |
| |
|
Tel: +49 821 598 2210 |
| |
|
Fax: +49 821 598 2280 |
| |
|
email: Lothar.Heinrich@Math.Uni-Augsburg.DE |
| |
|
|
| Dohy |
HONG |
Ecole Polytechnique |
| |
|
CMAP |
| |
|
D-91128 Palaiseau |
| |
|
France |
| |
|
email: dohy@cmapx.polytechnique.fr |
| |
|
|
| Juerg |
HUESLER |
University of Bern |
| |
|
IMSV |
| |
|
Sidklerstr. 5 |
| |
|
CH-3012 Bern |
| |
|
Switzerland |
| |
|
Tel: +31 631 88 10 |
| |
|
Fax: +31 631 38 70 |
| |
|
email: huesler@math-stat.unibe.ch |
| |
|
|
| Valerie |
ISHAM |
University College London |
| |
|
Dept. of Statistical Science |
| |
|
Gower Street |
| |
|
London WC1E 6BT |
| |
|
England |
| |
|
Tel: +44 171 419 3602 |
| |
|
Fax: +44 171 383 4703 |
| |
|
email: valerie@stats.ucl.ac.uk |
| |
|
|
| Predrag |
JELENKOVIC |
Room 2C-361, Bell Laboratories |
| |
|
Innovations for Lucent Technologies |
| |
|
600 Mountain Avenue |
| |
|
Murray Hill, NJ 07974 |
| |
|
USA |
| |
|
Tel: +1 908 582 7808 |
| |
|
Fax: +1 908 582 3340 |
| |
|
email: predrag@research.bell-labs.com |
| |
|
|
| Thomas |
KAEMPKE |
FAW Ulm |
| |
|
Helmholtzstr. 16 |
| |
|
D-89081 Ulm |
| |
|
Germany |
| |
|
Tel: +49 731 501 665 |
| |
|
Fax: +49 731 501 999 |
| |
|
email: kaempke@faw.uni-ulm.de |
| |
|
|
| Jaakob |
KIND |
Aachen University of Technology |
| |
|
Institute of Statistics |
| |
|
Wuellnerstr. 3 |
| |
|
D-52056 Aachen |
| |
|
Germany |
| |
|
Fax: +49 241 8888130 |
| |
|
email: kind@stochastik.rwth-aachen.de |
| |
|
|
| Maurice |
KLEIN |
France Telecom-CNET |
| |
|
38-40, rue du Gl. Leclerc |
| |
|
F-92131 Issy Les Moulineaux |
| |
|
France |
| |
|
Tel: +33 01 45 29 41 61 |
| |
|
Fax: +33 01 45 29 65 56 |
| |
|
email: klein@cnet.francetelecom.fr |
| |
|
|
| Udo |
KRIEGER |
Deutsche Telekom |
| |
|
Technologiezentrum |
| |
|
Am Kavalleriesand 3 |
| |
|
D-64295 Darmstadt |
| |
|
Germany |
| |
|
Tel: +49 6151 83 3835 |
| |
|
Fax: +49 6151 83 4575 |
| |
|
email: kriegeru@tzd.telekom.de |
| |
|
|
| Guenther |
LAST |
Technical University of Braunschweig |
| |
|
Institute of Mathematical Stochastics |
| |
|
Postfach 3329 |
| |
|
D-38023 Braunschweig |
| |
|
Germany |
| |
|
Tel: +49 531 391 7572 |
| |
|
Fax: +49 531 391 4577 |
| |
|
email: g.last@tu-bs.de |
| |
|
|
| Guy |
LATOUCHE |
Universite Libre De Bruxelles |
| |
|
ULB - Departement Informatique |
| |
|
CP 212, Boulevard du Triomphe |
| |
|
B-1050 Bruxelles |
| |
|
Belgium |
| |
|
Tel: +32 2 650 55 97 |
| |
|
Fax: +32 2 650 56 09 |
| |
|
email Guy.Latouche@ulb.ac.be |
| |
|
|
| Marc |
LEBOURGES |
France Telecom |
| |
|
DPS/SPE B 16 |
| |
|
6 Place d'Alleray |
| |
|
Annexe Brancion |
| |
|
F-75505 Paris Cedex 15 |
| |
|
France |
| |
|
email: marc.lebourges@francetelecom.fr |
| |
|
|
| Isabelle |
LE MADEC |
France Telecom - CNET DAC/GTR |
| |
|
38-40, rue du General Leclerc |
| |
|
F-92794 Issy-Moulineaux Cedex 9 |
| |
|
France |
| |
|
Tel: +33 01 45 29 60 18 |
| |
|
Fax: +33 01 45 29 65 56 |
| |
|
email: isabelle.lemadec@cnet.francetelecom.fr |
| |
|
|
| Armand |
MAKOWSKI |
University of Maryland |
| |
|
Electrical Engineering Dept. |
| |
|
College Park |
| |
|
Maryland 20742 |
| |
|
USA |
| |
|
Tel: +1 301 405 6844 |
| |
|
Fax: +1 301 314 9281 |
| |
|
email: armand@Glue.umd.edu |
| |
|
|
| Petteri |
MANNERSALO |
VTT Information Technology |
| |
|
P.O.Box 1202 |
| |
|
Otakaari 7 B, Espoo |
| |
|
FIN-02044 VTT |
| |
|
Finland |
| |
|
Tel: +358 9 456 5927 |
| |
|
Fax: +358 9 456 7013 |
| |
|
email: Petteri.Mannersalo@vtt.fi |
| |
|
|
| William |
MASSEY |
Math. Sci. Research Center |
| |
|
Bell Lab. of Lucent Technologies |
| |
|
700 Mountain Avenue |
| |
|
Room 2C-320 |
| |
|
Murray Hill, NJ 07974 - 0636 |
| |
|
USA |
| |
|
Tel: +1 908 582 3225 |
| |
|
Fax: +1 908 582 3340 |
| |
|
email: will@research.bell-labs.com |
| |
|
|
| Rudolf |
MATHAR |
Aachen University of Technology |
| |
|
Institute of Statistics |
| |
|
Wuellnerstr. 3 |
| |
|
D-52056 Aachen |
| |
|
Germany |
| |
|
Tel: +49 241 804576 |
| |
|
Fax: +49 241 8888130 |
| |
|
email: r.mathar@stochastik.rwth-aachen.de |
| |
|
|
| Bo Friis |
NIELSEN |
Dept. of Mathematical Modelling |
| |
|
Technical Univ. of Denmark |
| |
|
bldg. 321 |
| |
|
DK-2800 Lyngby |
| |
|
Denmark |
| |
|
Tel: +45 45 25 33 97 |
| |
|
Fax: +45 45 88 13 97 |
| |
|
email: bfn@imm.dtu.dk |
| |
|
|
| Ilkka |
NORROS |
VTT Information Technology |
| |
|
P.O.Box 1202 |
| |
|
FIN-02044 VTI |
| |
|
Finland |
| |
|
email: ilkka.norros@vtt.fi |
| |
|
|
| Sverrir |
OLAFSSON |
British Telecom Research Laboratories |
| |
|
Complexity Group |
| |
|
Admin2, pp5 |
| |
|
Martlesham Heath |
| |
|
Ipswich, Suffolk IP5 3RE |
| |
|
England |
| |
|
Tel: 01473 - 647410 |
| |
|
Tel: 01473 - 647410 |
| |
|
email: sverrir.olafsson@bt-sys.bt.co.uk |
| |
|
|
| Chong Jin |
PARK |
Dept. of Math. Computer Sci. |
| |
|
San Diego State University |
| |
|
San Diego CA 92182-7720 |
| |
|
USA |
| |
|
Tel: +1 619 594 6171 |
| |
|
email: cjpark@saturn.sdsu.edu |
| |
|
|
| Vaidyanathan |
RAMASWAMI |
AT& T Laboratories |
| |
|
Holmdel |
| |
|
USA |
| |
|
email: vramaswami@att.com |
| |
|
|
| Marie-Ange |
REMICHE |
Universite Libre De Bruxelles |
| |
|
ULB - Departement Informatique |
| |
|
CP 212, Boulevard du Triomphe |
| |
|
B-1050 Bruxelles |
| |
|
Belgium |
| |
|
Tel: +32 - 2 - 650 55 95 |
| |
|
Fax: +32 - 2 - 650 56 09 |
| |
|
email: mremiche@ulb.ac.be |
| |
|
|
| Tomasz |
ROLSKI |
Mathematical Institute |
| |
|
The University of Wroclaw |
| |
|
Pl. Grunwaldzki 2/4 |
| |
|
PL-50-384 Wroclaw |
| |
|
Poland |
| |
|
Tel: +48 71 204403 |
| |
|
email: rolski@math.uni.wroc.pl |
| |
|
|
| Rolf |
SCHASSBERGER |
Technical University of Braunschweig |
| |
|
Institute of Mathematical Stochastics |
| |
|
Postfach 3329 |
| |
|
D-38023 Braunschweig |
| |
|
Germany |
| |
|
Tel: +49 531 391 7565 |
| |
|
Fax: +49 531 391 4577 |
| |
|
email: r.schassberger@tu-bs.de |
| |
|
|
| Volker |
SCHMIDT |
University of Ulm |
| |
|
Institute of Stochastics |
| |
|
Helmholtzstr. 18 |
| |
|
D-89069 Ulm |
| |
|
Germany |
| |
|
Tel: +49 731 502 3532 |
| |
|
Fax: +49 731 502 3649 |
| |
|
email: schmidt@mathematik.uni-ulm.de |
| |
|
|
| Richard |
SERFOZO |
School of Industrial Engineering |
| |
|
Georgia Institute of Technology |
| |
|
Atlanta, Georgia 30324 |
| |
|
USA |
| |
|
Tel: +1 404 894 2305 |
| |
|
Fax: +1 404 894 2301 |
| |
|
email: rserfozo@isye.gatech.edu |
| |
|
|
| Alexander |
STOLYAR |
Motorola |
| |
|
1501 West Shure Drive, 1441 |
| |
|
Arlington Heights, IL 6000 |
| |
|
USA |
| |
|
Tel: +1 847 632-4662 |
| |
|
Fax: +1 847 632-2900 |
| |
|
email: stolyar@cig.mot.com |
| |
|
|
| Peter |
TAYLOR |
University of Adelaide |
| |
|
South Australia 5005 |
| |
|
Tel: +61 8 8303 5413 |
| |
|
Fax: +61 8 8303 4395 |
| |
|
email: ptaylor@maths.adelaide.edu.au |
| |
|
|
| Kostya |
TCHOUMATCHENKO |
INRIA |
| |
|
2004, route des Lucioles |
| |
|
BP 93 |
| |
|
F-06902 Sophia Antipolis |
| |
|
France |
| |
|
Tel: +33 4 92 38 76 49 |
| |
|
Fax: +33 4 92 38 79 71 |
| |
|
email: ktchoum@sophia.inria.fr |
| |
|
|
| Kurt |
TUTSCHKU |
University of Wuerzburg |
| |
|
Institute of Computer Science |
| |
|
Am Hubland |
| |
|
D-97074 Wuerzburg |
| |
|
Germany |
| |
|
Tel: +49 931 888-5511 |
| |
|
Fax: +49 931 888-5601 |
| |
|
email: tutschku@informatik.uni-wuerzburg.de |
| |
|
|
| Gideon |
WEISS |
Department of Statistics |
| |
|
University of Haifa |
| |
|
Mt. Carmel |
| |
|
Haifa 31905 |
| |
|
Israel |
| |
|
Tel: +972 4 8249004 |
| |
|
Fax: +972 4 8253849 |
| |
|
email: gweiss@stat.haifa.ac.il |
| |
|
|
| Sergei |
ZUYEV |
INRIA |
| |
|
2004, route des Lucioles |
| |
|
BP 93 |
| |
|
F-06902 Sophia Antipolis |
| |
|
France |
| |
|
Tel: +33 4 92 38 77 51 |
| |
|
Fax: +33 4 92 38 79 71 |
| |
|
email: sergei@sophia.inria.fr |
Andreas Frey
April 6, 1998
![]() of the positions of all other waiting users and the server's position.
The time needed to move from one user to the next will be neglected.
of the positions of all other waiting users and the server's position.
The time needed to move from one user to the next will be neglected.
![]() ,where
,where ![]() is the intensity of the underlying Poisson process, and we give a recursion
formula for the coefficients ai. Furthermore, we derive
an approximation of the same kind for the distribution of the sum V
of the uncovered parts in a given interval.
is the intensity of the underlying Poisson process, and we give a recursion
formula for the coefficients ai. Furthermore, we derive
an approximation of the same kind for the distribution of the sum V
of the uncovered parts in a given interval.
![]() aszczyszyn,
E. Merzbach and V. Schmidt (1997) A note on expansion for functionals
of spatial marked point processes. Statistics and Probability Letters
36, 299-306.
aszczyszyn,
E. Merzbach and V. Schmidt (1997) A note on expansion for functionals
of spatial marked point processes. Statistics and Probability Letters
36, 299-306.
![]() and
and ![]() with error terms exponentially small in x uniformly in
with error terms exponentially small in x uniformly in ![]() ,
where T is any fixed positive constant. We prove that, as
,
where T is any fixed positive constant. We prove that, as ![]() ,
, ![]() ,
, ![]() ,uniformly
in
,uniformly
in ![]() ,where
,where ![]() and
and ![]() are given by explicit, albeit complicated formulas. Using these asymptotic
estimates we show that Nx(t) satisfies a central
limit theorem, i.e., for any fixed t
are given by explicit, albeit complicated formulas. Using these asymptotic
estimates we show that Nx(t) satisfies a central
limit theorem, i.e., for any fixed t