University of Ulm, Faculty of Mathematics and Economics

The Design of a Fuzzy-Shewhart Control Chart

Department of Stochastics

General Information

Author:	J. Höppner and H. Wolff
Appeared in:	Research Report 52 of the Würzburg Research Group on Quality Control, 1995
Contact:	wolff@mathematik.uni-ulm.de

Abstract

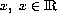In this paper we suggest a design for a control chart in the case of vague data. Such data may arise in form of linguistic data or by imprecise measurements, which all can modelled by fuzzy - sets. We consider fuzzy - sets as real valued interpretations of vague data. We leave the traditional approach that we are always able to assign exactly one real number (or p-dimensional vectors) to the outcome of our experiment. Indeed, if we have to meet uncertainty and vagueness in describing our observations, we should replace the classical dichotomous judgements (we observe

) by introducing fuzzy - sets, which themselves can be described by membership functions. For quality purposes, such an approach is described in more detail e.g. in Laviolette et al.
Our starting point is based on the pioneering work of L.A.Zadeh on fuzzy - sets and his extension principle as well as on the concept of a fuzzyrandom variable introduced by Kwakernaak. The generalization of traditional control charts to the ''fuzzy case'' will be studied in this paper for the simple Shewhart chart. The statistics involved in Shewhart chart techniques are the mean and the variance of a random sample. Therefore, we need a generalization of such statistics for fuzzy random samples. The corresponding statistics can be found e.g. in the excellent book of R.Kruse and K.D.Meyer, which gives a thorough discussion of statistical methods for fuzzy - data.
Even for Shewhart charts, we will see that in case of fuzzy - data the stopping rule will not be as simple as in the traditional case. Simultaneous test problems arise implying e.g. difficulties for an exact evaluation of the operating characteristic function or the average run length.

Download

Download dvi version (204 KB)
Download Postscript version (442 KB)

Alexander Schöne -- Last update: May 15, 1997