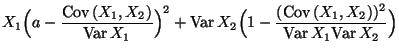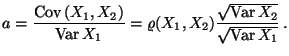Next: Erwartungswertvektor und Kovarianzmatrix
Up: Gemischte Momente
Previous: Multiplikationsformel und Kovarianz
Contents
Linearer Zusammenhang von Zufallsvariablen
Die Korrelation
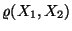 zweier Zufallsvariablen
zweier Zufallsvariablen
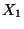 und
und 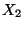 mit
mit
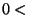 Var
Var 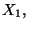 Var
Var 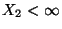 kann man als Grad ihres linearen (stochastischen) ,,Zusammenhanges'' auffassen.
kann man als Grad ihres linearen (stochastischen) ,,Zusammenhanges'' auffassen.
Eine genauere Formulierung dieses Phänomens liefert
- Theorem 4.12
 Seien
Seien
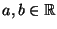 beliebige Zahlen, und
beliebige Zahlen, und 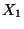 ,
, 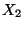 seien Zufallsvariable mit
seien Zufallsvariable mit
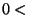 Var
Var 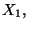 Var
Var 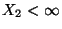 .
.
- Die erwartete quadratische Abweichung
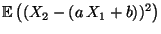 zwischen den
Zufallsvariablen
zwischen den
Zufallsvariablen 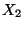 und
und 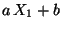 ist minimal, wenn
ist minimal, wenn 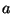 und
und 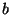 wie folgt gewählt werden:
wie folgt gewählt werden:
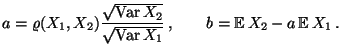 |
(30) |
- Insbesondere gilt
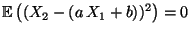 , d.h.
, d.h.
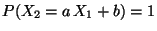 genau dann, wenn
genau dann, wenn
- Beweis





Next: Erwartungswertvektor und Kovarianzmatrix
Up: Gemischte Momente
Previous: Multiplikationsformel und Kovarianz
Contents
Roland Maier
2001-08-20
![]() zweier Zufallsvariablen
zweier Zufallsvariablen
![]() und
und ![]() mit
mit
![]() Var
Var ![]() Var
Var ![]() kann man als Grad ihres linearen (stochastischen) ,,Zusammenhanges'' auffassen.
kann man als Grad ihres linearen (stochastischen) ,,Zusammenhanges'' auffassen.