



Next: Schätzung von Parametern
Up: Grundideen der statistischen Datenanalyse
Previous: Stichprobenvarianz
Contents
Empirische Verteilungsfunktion
Außer der Schätzung von Erwartungswert 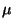 und Varianz
und Varianz
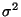 der Stichprobenvariablen
der Stichprobenvariablen 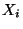 kann auch deren
Verteilungsfunktion
kann auch deren
Verteilungsfunktion 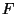 aus den vorliegenden Daten
aus den vorliegenden Daten
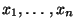 geschätzt werden.
geschätzt werden.
- Beachte
-
- Man kann sich leicht überlegen, daß für jeden Vektor
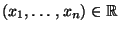 die Abbildung
die Abbildung
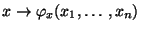 |
(15) |
die Eigenschaften einer Verteilungsfunktion hat.
- Die in (15) gegebene Abbildung wird deshalb
empirische Verteilungsfunktion der (konkreten)
Stichprobe
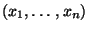 genannt.
genannt.
Dies führt zu der folgenden Begriffsbildung.
- Definition 5.9
 Die Abbildung
Die Abbildung
![$ \hat F_n:\mathbb{R}\times\Omega\to[0,1]$](img1203.png) mit
mit
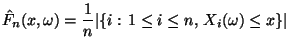 |
(16) |
heißt empirische Verteilungsfunktion der Zufallsstichprobe
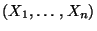 .
.
- Beachte
-
- Die in (16) gegebene Abbildung
kann man als eine Familie
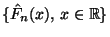 von
Zufallvariablen
von
Zufallvariablen
![$ \hat F_n(x):\Omega\to[0,1]$](img1206.png) auffassen.
auffassen.
- Eine solche Familie von Zufallsvariablen wird empirischer Prozeß
genannt.
- Empirische Prozesse sind eine spezielle Klasse stochastischer Prozesse.
- Theorem 5.10
 Für jedes
Für jedes
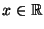 gilt:
gilt:
- Die Zufallsvariable
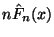 ist binomialverteilt
mit den Parametern
ist binomialverteilt
mit den Parametern 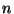 und
und 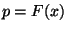 . D.h., für
. D.h., für
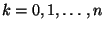 gilt
gilt
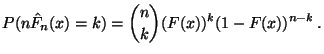 |
(17) |
- Insbesondere gilt also
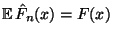 und Var und Var 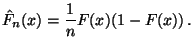 |
(18) |
-
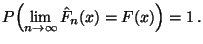 |
(19) |
- Falls
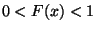 , dann gilt außerdem für jedes
, dann gilt außerdem für jedes
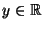
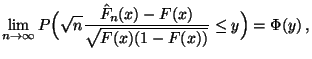 |
(20) |
wobei 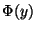 die Verteilungsfunktion der
Standardnormalverteilung ist.
die Verteilungsfunktion der
Standardnormalverteilung ist.
- Beweis
-
- Wegen (16) können wir die Zufallsvariable
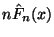 als die Anzahl der Erfolge beim
als die Anzahl der Erfolge beim 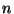 -maligen
Münzwurf mit den identischen Erfolgswahrscheinlichkeiten
-maligen
Münzwurf mit den identischen Erfolgswahrscheinlichkeiten
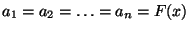 auffassen, vgl. Beispiel 2 in
Abschnitt 3.2.2. Hieraus ergibt sich
(17).
auffassen, vgl. Beispiel 2 in
Abschnitt 3.2.2. Hieraus ergibt sich
(17).
- Damit ist auch (18) bewiesen, vgl.
Beispiel 1 in den Abschnitten 4.1.1 und
4.1.2.
- Wegen der Darstellungsmöglichkeit von
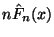 als die Anzahl der Erfolge beim
als die Anzahl der Erfolge beim 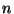 -maligen
Münzwurf mit identischen Erfolgswahrscheinlichkeiten ist
-maligen
Münzwurf mit identischen Erfolgswahrscheinlichkeiten ist
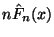 die Summe von
die Summe von 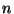 unabhängigen und identisch
(Bernoulli-) verteilten Zufallsvariablen. Deshalb ergibt sich
(19) aus dem starken Gesetz der großen Zahlen (vgl.
Theorem 4.22).
unabhängigen und identisch
(Bernoulli-) verteilten Zufallsvariablen. Deshalb ergibt sich
(19) aus dem starken Gesetz der großen Zahlen (vgl.
Theorem 4.22).
- Mit der gleichen Begründung ergibt sich (20) unmittelbar aus
dem zentralen Grenzwertsatz (vgl. Theorem 4.24).
- Beachte
-
- Weil die Zufallsvariable
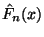 den Erwartungswert
den Erwartungswert
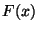 hat (vgl. (18), kann
hat (vgl. (18), kann
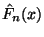 als ein geeigneter Schätzer von
als ein geeigneter Schätzer von 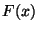 angesehen werden.
angesehen werden.
- Neben der fast sicheren Konvergenz (19), die
für jedes (einzelne)
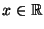 gilt, kann man zeigen, daß sich
auch die Verteilungsfunktion
gilt, kann man zeigen, daß sich
auch die Verteilungsfunktion 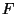 insgesamt durch den
empirischen Prozeß
insgesamt durch den
empirischen Prozeß
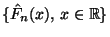 im Sinne der
fast sicheren Konvergenz approximieren läßt.
im Sinne der
fast sicheren Konvergenz approximieren läßt.
- Dabei ist die folgende Verschärfung des starken Gesetzes der
großen Zahlen gemeint, die in der Literatur Satz von
Gliwenko/Cantelli genannt wird.
- Theorem 5.11
 Sei
Sei
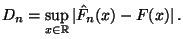 |
(21) |
Dann gilt
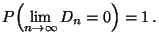 |
(22) |
- Beweis
 Der Beweis von Theorem 5.11 ist tiefliegend und
geht über den Rahmen dieser einführenden Vorlesung hinaus.
Der Beweis von Theorem 5.11 ist tiefliegend und
geht über den Rahmen dieser einführenden Vorlesung hinaus.
- Beachte
 Ein JAVA-Applet, mit dem die Aussage des Satzes von
Gliwenko/Cantelli, d.h. der Grenzübergang
(22) simuliert werden kann, findet man
beispielsweise auf der Internet-Seite:
Dieses JAVA-Applet simuliert die empirische
Verteilungsfunktion
Ein JAVA-Applet, mit dem die Aussage des Satzes von
Gliwenko/Cantelli, d.h. der Grenzübergang
(22) simuliert werden kann, findet man
beispielsweise auf der Internet-Seite:
Dieses JAVA-Applet simuliert die empirische
Verteilungsfunktion 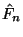 für den Fall, daß
für den Fall, daß
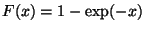 für
für 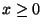 , d.h.,
, d.h., 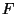 ist die Verteilungsfunktion der
Exponentialverteilung Exp
ist die Verteilungsfunktion der
Exponentialverteilung Exp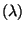 mit dem Parameter
mit dem Parameter 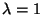 .
.
Ähnlich wie beim zentralen Grenzwertsatz für Summen von
unabhängigen und identisch verteilten Zufallsvariablen (vgl.
Theorem 4.24) kann man zeigen, daß auch 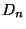 bei entsprechend
gewählter Normierung gegen einen nichtdeterministischen, d.h.
zufälligen Grenzwert (im Sinne der Verteilungskonvergenz) strebt.
bei entsprechend
gewählter Normierung gegen einen nichtdeterministischen, d.h.
zufälligen Grenzwert (im Sinne der Verteilungskonvergenz) strebt.
Dies ist die Aussage des folgenden Theorems, das Satz von
Kolmogorow/Smirnow genannt wird.
- Theorem 5.12
 Falls die Verteilungsfunktion
Falls die Verteilungsfunktion 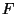 der
Stichprobenvariablen
der
Stichprobenvariablen 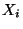 ein stetige Funktion ist, dann gilt für
ein stetige Funktion ist, dann gilt für
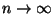
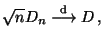 |
(23) |
wobei 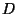 eine Zufallsvariable ist, deren Verteilungsfunktion
gegeben ist durch
eine Zufallsvariable ist, deren Verteilungsfunktion
gegeben ist durch
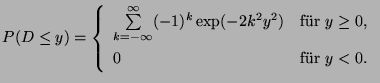 |
(24) |
- Beweis
 Der Beweis von Theorem 5.12 ist tiefliegend und
geht über den Rahmen dieser einführenden Vorlesung hinaus.
Der Beweis von Theorem 5.12 ist tiefliegend und
geht über den Rahmen dieser einführenden Vorlesung hinaus.




Next: Schätzung von Parametern
Up: Grundideen der statistischen Datenanalyse
Previous: Stichprobenvarianz
Contents
Roland Maier
2001-08-20
![]() und Varianz
und Varianz
![]() der Stichprobenvariablen
der Stichprobenvariablen ![]() kann auch deren
Verteilungsfunktion
kann auch deren
Verteilungsfunktion ![]() aus den vorliegenden Daten
aus den vorliegenden Daten
![]() geschätzt werden.
geschätzt werden.
![]() bei entsprechend
gewählter Normierung gegen einen nichtdeterministischen, d.h.
zufälligen Grenzwert (im Sinne der Verteilungskonvergenz) strebt.
bei entsprechend
gewählter Normierung gegen einen nichtdeterministischen, d.h.
zufälligen Grenzwert (im Sinne der Verteilungskonvergenz) strebt.