Nächste Seite: Kopplungsalgorithmen; perfekte MCMC-Simulation
Aufwärts: Fehleranalyse bei MCMC-Simulation
Vorherige Seite: MCMC-Schätzer; Bias und Fundamentalmatrix
Inhalt
Asymptotische Schätzvarianz; mittlerer quadratischer Fehler
Für das in Abschnitt 3.4.2 eingeführte statistische
Modell untersuchen wir nun das asymptotische Verhalten der Varianz
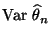 , wenn
, wenn
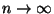 .
.
Theorem 3.19

Es gilt
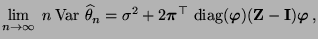 |
(78) |
wobei
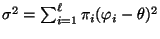
und
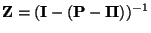
die in
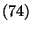
definierte Fundamentalmatrix von

ist.
- Beweis
-
- Offenbar gilt
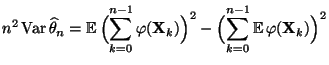 |
(79) |
und somit
- Wir nutzen nun diese Darstellungsformel, um die Gültigkeit von
(78) zunächst für den Fall
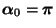 zu
zeigen.
zu
zeigen.
- In diesem Fall gilt nämlich, dass
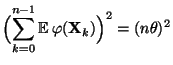
und
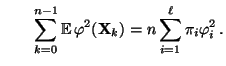
- Außerdem ergibt sich dann aus der Stationarität der Markov-Kette
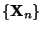 , dass
wobei
und
, dass
wobei
und
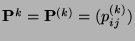 die Matrix der
die Matrix der
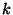 -stufigen Übergangswahrscheinlichkeiten bezeichnet.
-stufigen Übergangswahrscheinlichkeiten bezeichnet.
- Hieraus folgt nun insgesamt, dass
- wobei in der zweiten Gleichheit die folgende Identität genutzt
wurde:
- Hieraus ergibt sich (78), wenn dabei die
Darstellungsformel (76) für
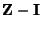 berücksichtigt wird.
berücksichtigt wird.
- Wir zeigen nun noch, dass (78) auch für jede
beliebige Anfangsverteilung
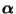 gilt.
gilt.
- Dabei präzisieren wir die Bezeichnungsweise wie folgt: Wir
schreiben
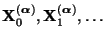 anstelle von
anstelle von
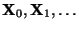 bzw.
bzw.
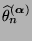 anstelle von
anstelle von
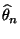 .
.
- Es genügt zu zeigen, dass
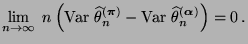 |
(80) |
- Hierfür führen wir noch die folgenden Bezeichnungen ein: Für
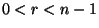 sei
sei
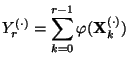
und
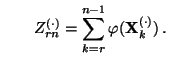
- Dann ergibt sich aus (79), dass
wobei wir die drei Summanden des letzten Ausdruckes mit 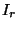 ,
,
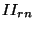 bzw.
bzw. 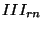 bezeichnen.
bezeichnen.
- Der Summand
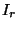 hängt nicht von
hängt nicht von 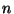 ab, weshalb
ab, weshalb
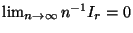 .
.
- Weil der Zustandsraum
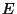 endlich ist, gilt für die Konstante
endlich ist, gilt für die Konstante
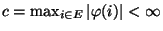 , dass
, dass
- Hieraus folgt, dass
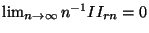 für jedes
für jedes
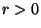 , weil mit Wahrscheinlichkeit
, weil mit Wahrscheinlichkeit 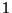 für jedes
für jedes 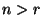 und
und
- Außerdem gilt für
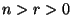 die Abschätzung
die Abschätzung
wobei man sich leicht überlegen kann, dass das Supremum endlich
ist.
- Weil die letzte Summe wegen der Ergodizität der Markov-Kette
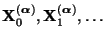 beliebig
klein wird, falls
beliebig
klein wird, falls 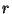 hinreichend groß ist, ist damit die
Gültigkeit von (80) bewiesen.
hinreichend groß ist, ist damit die
Gültigkeit von (80) bewiesen.

- Beachte
-
- Zur Erinnerung
- Die beiden Summanden auf der rechten Seite von
(81) konvergieren unterschiedlich schnell gegen
0, wenn
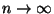 .
.
- In Theorem 3.19 haben wir gezeigt, dass
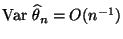 gilt.
gilt.
- Andererseits ergibt sich aus Theorem 3.18, dass
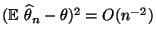 .
.
- Hieraus folgt, dass
- nicht der Bias
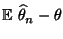 , sondern die
asymptotische Varianz
, sondern die
asymptotische Varianz
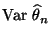 des Schätzers
des Schätzers
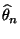
- die entscheidende Rolle bei der asymptotischen Analyse des
MQ-Fehlers
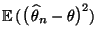 des in
(70) definierten MCMC-Schätzers
des in
(70) definierten MCMC-Schätzers
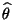 spielt, wenn
spielt, wenn
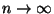 .
.
- Mit anderen Worten: Es kann sinnvoll sein, die Simulationsmatrix
 so zu wählen,
so zu wählen,
- dass die asymptotische Schätzvarianz
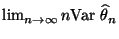 möglichst klein ist,
möglichst klein ist,
- gegebenenfalls bei einer gewissen Vergrößerung des asymptotischen
Bias
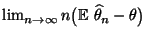 .
.
Um diese Problematik näher zu untersuchen, führen wir die folgende
Bezeichnung ein: Sei
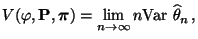
wobei
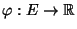 eine beliebige Funktion und
eine beliebige Funktion und
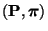 ein beliebiges reversibles Paar ist.
ein beliebiges reversibles Paar ist.
- Beweis
-
- Sei
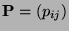 eine Übergangsmatrix, so dass das Paar
eine Übergangsmatrix, so dass das Paar
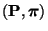 reversibel ist. Es genügt zu zeigen, dass
reversibel ist. Es genügt zu zeigen, dass
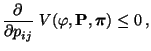 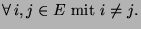 |
(83) |
- Aus Theorem 3.19 ergibt sich, dass
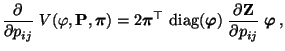 |
(84) |
wobei
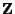 die in (74) eingeführte
Fundamentalmatrix von
die in (74) eingeführte
Fundamentalmatrix von
 ist.
ist.
- Andererseits folgt aus
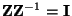 , dass
und somit
, dass
und somit
- Hieraus und aus (84) ergibt sich, dass
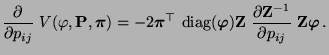 |
(85) |
- Weil das Paar
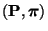 reversibel ist, ergibt sich aus der
in Lemma 3.3 hergeleiteten Darstellungsformel
(75) für die Fundamentalmatrix
reversibel ist, ergibt sich aus der
in Lemma 3.3 hergeleiteten Darstellungsformel
(75) für die Fundamentalmatrix
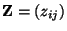 , dass
für beliebige
, dass
für beliebige 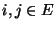
- Hieraus folgt, dass
- Somit ergibt sich aus (85), dass
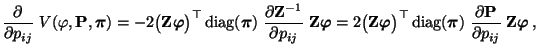 |
(86) |
wobei in der letzten Gleichheit die Identität
genutzt wurde, die sich unmittelbar aus der Definitionsgleichung
(74) von
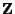 ergibt.
ergibt.
- Weil
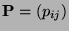 eine stochastische Matrix ist und weil das
Paar
eine stochastische Matrix ist und weil das
Paar
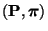 reversibel ist,
reversibel ist,
- Damit ist die Gültigkeit von (83) bewiesen.

- Beachte
 Aus Theorem 3.20 folgt insbesondere,
Aus Theorem 3.20 folgt insbesondere,
- dass durch die Simulationsmatrix
 des
Metropolis-Algorithmus (d.h, wenn in (50) die
Gleichheit betrachtet wird) die asymptotische Varianz
des
Metropolis-Algorithmus (d.h, wenn in (50) die
Gleichheit betrachtet wird) die asymptotische Varianz
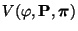 minimiert wird,
minimiert wird,
- und zwar in der Klasse aller Metropolis-Hastings-Algorithmen mit
einer beliebigen, jedoch fest vorgegebenen ,,potentiellen
Übergangsmatrix''
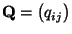 .
.




Nächste Seite: Kopplungsalgorithmen; perfekte MCMC-Simulation
Aufwärts: Fehleranalyse bei MCMC-Simulation
Vorherige Seite: MCMC-Schätzer; Bias und Fundamentalmatrix
Inhalt
Ursa Pantle
2003-09-29
![]() , wenn
, wenn
![]() .
.
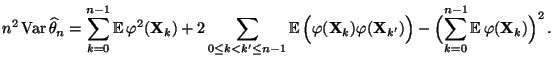
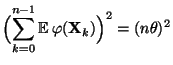 und
und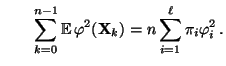
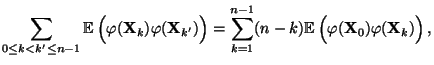
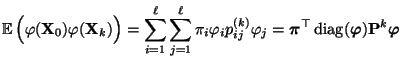
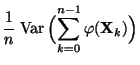
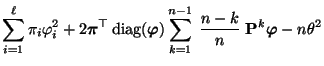
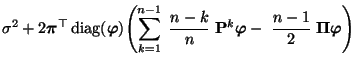
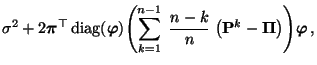
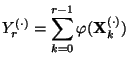 und
und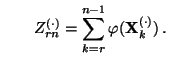
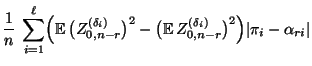
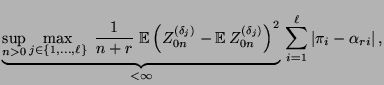
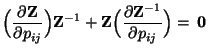
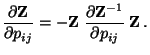
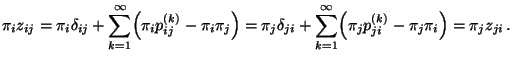
![\begin{displaymath}
\Bigl({\,{\rm diag}}({\boldsymbol{\pi}}) \;\frac{\partial {\...
...me)=(j,i)$,}\\ [3\jot]
0\,, &\mbox{sonst.}
\end{array}\right.
\end{displaymath}](img1918.png)