wobei
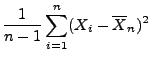 |
|||
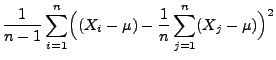 |
|||
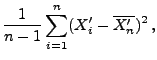 |
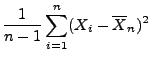 |
|||
 |
|||
 |
 |
|||
 |
|||
 |
 |
 |
||
 |
|||
 |
|||
 |
|||
 |
 |
||
 |
|||
 |
|||
 |
|||
 |
 |
|||
 |
|||
 |
|||
 |
|||
 |
 |
|||
Neben den Formeln (10) und (11) für
Erwartungswert und Varianz des Stichprobenvarianz ![]() sind
erneut weitere Aussagen über die Verteilung von
sind
erneut weitere Aussagen über die Verteilung von ![]() bzw. über
deren asymptotisches Verhalten für große
bzw. über
deren asymptotisches Verhalten für große ![]() von Interesse.
von Interesse.
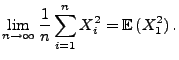
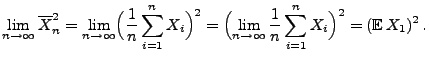
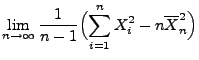 |
|||
 |
|||
 |
|||
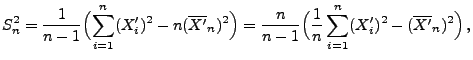
 |
 |
||
 |
|||
 |
|||
 |
 |
||
 |
|||