



Next: Example: Hard-Core Model
Up: Monte-Carlo Simulation
Previous: Quotients of Uniformly Distributed
Contents
Simulation Methods Based on Markov Chains
- Remarks
-
- An alternative simulation method is based on
- constructing a Markov chain
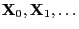 with state
space
with state
space 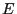
- and an (appropriately chosen) irreducible and aperiodic transition
matrix
 ,
,
- such that
 is the ergodic limit distribution of the Markov
chain.
is the ergodic limit distribution of the Markov
chain.
- For sufficiently large

-
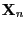 is approximately
is approximately
 -distributed
-distributed
- and can thus serve as an efficient tool for the generation of
(approximately)
 -distributed pseudo-random elements in
-distributed pseudo-random elements in
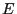 .
.
- Therefore one also uses the term Markov-Chain-Monte-Carlo
Simulation (MCMC).
Subsections




Next: Example: Hard-Core Model
Up: Monte-Carlo Simulation
Previous: Quotients of Uniformly Distributed
Contents
Ursa Pantle
2006-07-20
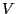 is a finite set of pixels
is a finite set of pixels
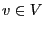 in the observation window
in the observation window 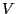 gets mapped
to a greyscale value
gets mapped
to a greyscale value 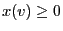 ,
,
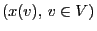 that has certain
properties.
that has certain
properties.
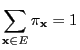 and
and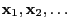 in
in 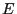 that are distributed according to
that are distributed according to
 .
.