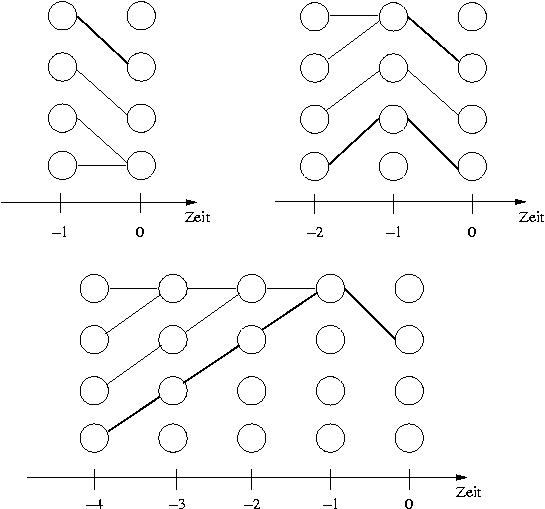
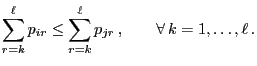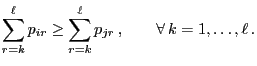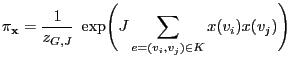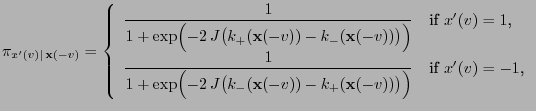- The update function
![$ \varphi:E\times(0,1]\to E$](img173.png) defined in
(88) satisfies the monotonicity condition
(91)
defined in
(88) satisfies the monotonicity condition
(91)
- if the state space can identified with the set
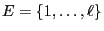 equipped with the natural order
equipped with the natural order  of the
numbers
of the
numbers
- and if the simulation matrix
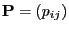 is monotonously nondecreasing with respect to the order
is monotonously nondecreasing with respect to the order 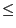 , i.e.,
for arbitrary
, i.e.,
for arbitrary 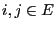 such that
such that 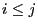 we have
we have
- if the state space can identified with the set
- A whole class of transition matrices
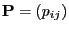 satisfying
the monotonicity condition (100) is given by the
tridiagonal matrices of birth-and-death processes which
are of the type
where
satisfying
the monotonicity condition (100) is given by the
tridiagonal matrices of birth-and-death processes which
are of the type
where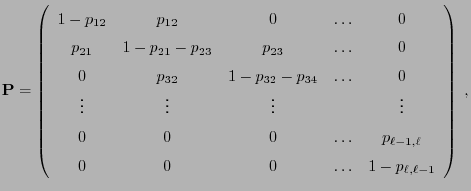
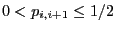 for all
for all
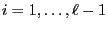 and
and
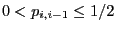 for all
for all
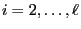 .
.
- On the other hand, the update function
![$ \varphi:E\times(0,1]\to E$](img173.png) defined in (88) is monotonously nonincreasing, see
(98),
defined in (88) is monotonously nonincreasing, see
(98),
- if
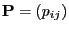 is monotonously nonincreasing with
respect to
is monotonously nonincreasing with
respect to 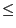 ,
,
- i.e., if for arbitrary
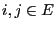 such that
such that 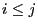 we have
we have
- if
- It is easy to show that there is no tridiagonal transition matrix
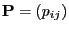 satisfying the condition (101),
i.e., birth-and-death processes are never monotonously
nonincreasing.
satisfying the condition (101),
i.e., birth-and-death processes are never monotonously
nonincreasing.
- However, condition (101) holds for example for the
following matrix:
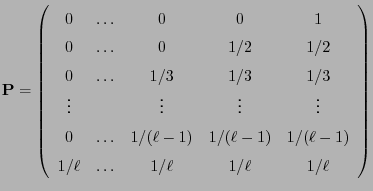
- Like for the hard-core model discussed in
Section 3.3.1
- we consider a connected graph
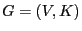 with finitely many vertices
with finitely many vertices
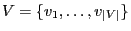
- and a certain set
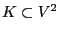 of edges
of edges
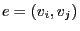 , each of
them connecting two vertices
, each of
them connecting two vertices 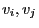 .
.
- we consider a connected graph
- One of the values
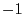 and
and 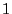 is assigned to each vertex,
is assigned to each vertex,
- and we consider the state space
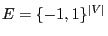 of all
configurations
of all
configurations
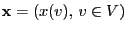 , i.e. for each
, i.e. for each 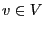 either
either 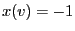 or
or 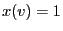 .
.
- If this is interpreted as an image,
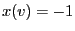 is regarded as a
white pixel and
is regarded as a
white pixel and 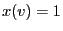 as a black pixel.
as a black pixel.
- and we consider the state space
- For each
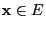 let the probability
let the probability
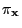 of the
configuration
of the
configuration
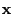 be given by
be given by
for a certain parameter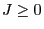 , which is interpreted as
,,inverse temperature'' in physics:
, which is interpreted as
,,inverse temperature'' in physics:
- For
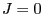 (infinite temperature) the distribution
(infinite temperature) the distribution
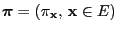 given by (102) is
the discrete uniform distribution.
given by (102) is
the discrete uniform distribution.
- For
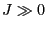 (low temperature) those configurations possess a large
probability that have a small number of connected pairs of vertices
being differently colored.
(low temperature) those configurations possess a large
probability that have a small number of connected pairs of vertices
being differently colored.
- For
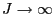 (zero temperature) the distribution
(zero temperature) the distribution
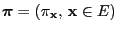 given by (102)
converges to the ,,two point uniform distribution''
given by (102)
converges to the ,,two point uniform distribution''
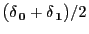 ,
,
- where
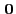 and
and
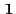 denote the (extreme) configurations
consisting either only of white or only of black pixels, i.e. either
denote the (extreme) configurations
consisting either only of white or only of black pixels, i.e. either
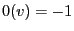 or
or 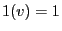 for all
for all 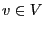 .
.
- For
- Notice that
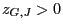 is an (in general unknown) normalizing
constant where
is an (in general unknown) normalizing
constant where
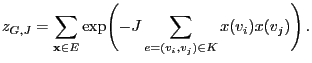
- The following figure was taken from O. Häggström (2002) Finite
Markov Chains and Algorithmic Applications, CU Press, Cambridge.
- It illustrates the role of the parameter
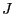 ,
,
- i.e., an increase of
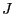 results in a more pronounced clumping
tendency of identically colored pixels.
results in a more pronounced clumping
tendency of identically colored pixels.
Figure 8: Typical configuration of the Ising model for 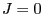 (upper
left corner),
(upper
left corner), 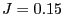 (upper right corner),
(upper right corner), 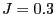 (lower left
corner) and
(lower left
corner) and 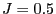 (lower right corner)
(lower right corner)
- It illustrates the role of the parameter
- Let the simulation matrix
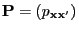 be given
by the Gibbs sampler, i.e., assume that (36) holds,
namely
be given
by the Gibbs sampler, i.e., assume that (36) holds,
namely
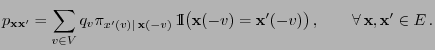
- where for arbitrary
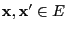 such that
such that
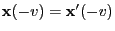 using the notation
using the notation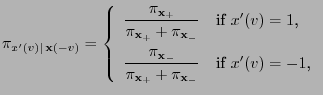
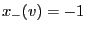 and
and
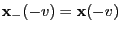 and
similarly
and
similarly 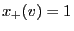 and
and
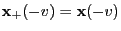 .
.
- By (102) we obtain for
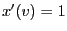 that
and in the same way for
that
and in the same way for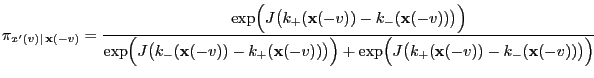
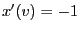 that
Thus, we can summarize
that
Thus, we can summarize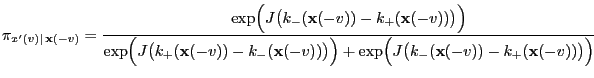
where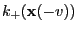 and
and
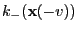 denote the number of
vertices connected to
denote the number of
vertices connected to 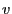 having the values
having the values 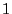 and
and 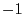 ,
respectively.
,
respectively.
- where for arbitrary
- For the state space
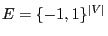 we define the partial order
we define the partial order
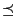
- by
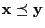 if
if
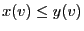 for all
for all 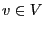 such that
such that
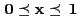 for all
for all
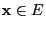 ,
,
- where we assume the elements of the state space
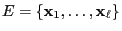 to be indexed in a way ensuring
to be indexed in a way ensuring
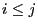 if
if
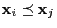 (this is e.g. the case if
(this is e.g. the case if 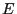 is ordered lexicographically).
is ordered lexicographically).
- by
- Then (103) implies for arbitrary
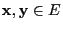 such that
such that
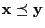
because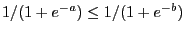 for arbitrary
for arbitrary
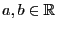 such that
such that 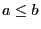 .
.
- Let the update function
![$ \varphi:E\times(0,1]^2\to E$](img2120.png) be given by
be given by
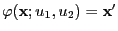 , where
, where
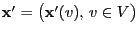 and for all
and for all
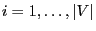
![$\displaystyle {\mathbf{x}}^\prime(v_i)=\left\{\begin{array}{ll} 1&\mbox{if
$\su...
...{x}}(-v_i)}$,}\\ [3\jot]
{\mathbf{x}}(v_i)\,,&\mbox{else.}
\end{array}\right.
$](img2123.png)