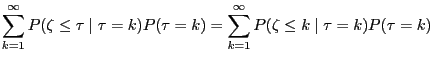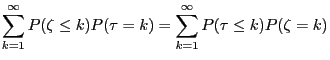- the necessity to save all innovations
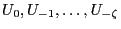 where
where 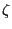 denotes the coupling
time defined in (95), i.e.
denotes the coupling
time defined in (95), i.e.
- Therefore, in the year 2000, David Wilson suggested the following modifications of the CFTP algorithm aiming at a reduction of the necessary memory allocation.
- based on a sequence of independent and identically distributed blocks of ,,forward simulation'', where
- the (potential) ,,initial times''
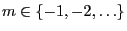 of the
Markov chain
of the
Markov chain
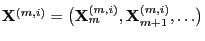 can be picked at random.
can be picked at random.
- For arbitrary
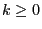 and
and
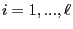 , let
, let
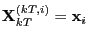 and
and
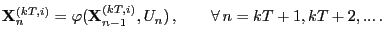
- Furthermore, for each
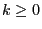 we consider the event
where the length
we consider the event
where the length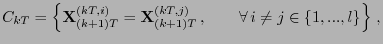
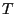 of the blocks is chosen such that
of the blocks is chosen such that
- Simulate
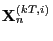 via
via 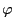 and
and
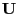 for
for
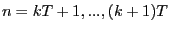 .
.
- Set
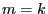 and
and 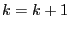 . If the event
. If the event 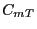 has occurred
proceed with step 3, otherwise return to step 1.
has occurred
proceed with step 3, otherwise return to step 1.
- Repeat steps 1 and 2 until the event
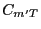 occurs for some
occurs for some
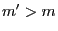 and return the value of
and return the value of
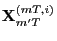 for an arbitrary
for an arbitrary
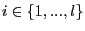 as a realization of
as a realization of
 .
.