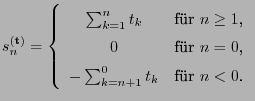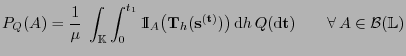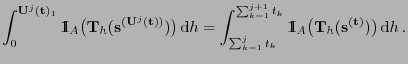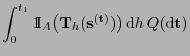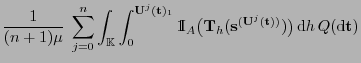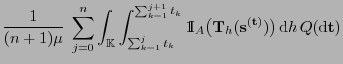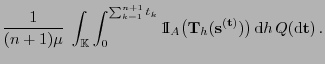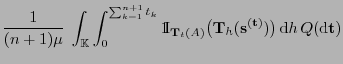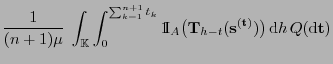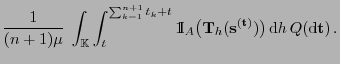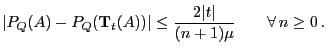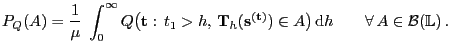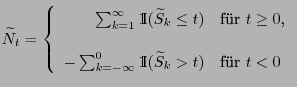Nächste Seite: Erneuerungsprozesse mit stationären Zuwächsen
Aufwärts: Zählprozesse im
Vorherige Seite: Homogener Poisson-Prozess
Inhalt
Allgemeines Konstruktionsprinzip für Zählprozesse
mit stationären Zuwächsen
- Der am Ende von Abschnitt 4.1.1 erwähnte Zuhammenhang
- zwischen (Poissonschen) Zählprozessen mit stationären Zuwächsen
und stationären Folgen von (unabhängigen und exponentiell
verteilten) Zwischenankunftszeiten
- kann als Spezialfall eines wesentlich allgemeineren Szenarios
aufgefasst werden.
- Dabei gehen wir nun umgekehrt vor und setzen voraus,
- dass
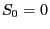 gilt und
gilt und
- dass die Zwischenankunftszeiten
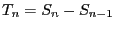 zwischen den
aufeinanderfolgenden Ereigniszeitpunkten
zwischen den
aufeinanderfolgenden Ereigniszeitpunkten 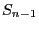 und
und 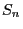 eine beliebige stationäre Folge
eine beliebige stationäre Folge 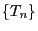 von (nichtnotwendig
unabhängigen) positiven Zufallsvariablen über einem gewissen
Wahrscheinlichkeitsraum
von (nichtnotwendig
unabhängigen) positiven Zufallsvariablen über einem gewissen
Wahrscheinlichkeitsraum
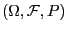 bilden.
bilden.
Es gelte also
 |
(6) |
und damit auch
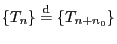 für jede natürliche Zahl
für jede natürliche Zahl 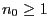 .
Außerdem setzen wir in diesem Abschnitt lediglich voraus, dass
.
Außerdem setzen wir in diesem Abschnitt lediglich voraus, dass
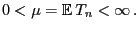 |
(7) |
- Beachte
-
- Es ist klar, dass die Invarianzeigenschaft (6)
insbesondere dann gilt, wenn
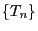 eine Folge von unabhängigen
und identisch verteilten Zufallsvariablen ist.
eine Folge von unabhängigen
und identisch verteilten Zufallsvariablen ist.
- Weitere Beispiele von stationären Folgen
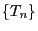 , die nicht aus unabhängigen Zufallsvariablen bestehen, lassen sich mit
Hilfe der Sprungzeitpunkte von reversiblen Markow-Prozessen
konstruieren, die ihre Werte in dem endlichen Zustandsraum
, die nicht aus unabhängigen Zufallsvariablen bestehen, lassen sich mit
Hilfe der Sprungzeitpunkte von reversiblen Markow-Prozessen
konstruieren, die ihre Werte in dem endlichen Zustandsraum
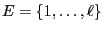 annehmen, wobei
annehmen, wobei 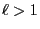 eine beliebige,
jedoch vorgegebene natürliche Zahl ist; vgl.
Abschnitt 4.1.4.
eine beliebige,
jedoch vorgegebene natürliche Zahl ist; vgl.
Abschnitt 4.1.4.
Wir zeigen nun, wie man ausgehend von einer stationären Folge
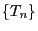 von positiven Zufallsvariablen über
von positiven Zufallsvariablen über
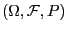 einen Wahrscheinlichkeitsraum
einen Wahrscheinlichkeitsraum
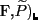 und einen
Zählprozess
und einen
Zählprozess
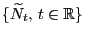 über
über
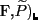 konstruieren
kann, so dass
konstruieren
kann, so dass
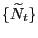 stationäre Zuwächse hat.
stationäre Zuwächse hat.
Hierfür führen wir zunächst einige Bezeichnungen ein.
- Mit
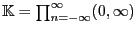 bezeichnen wir den
Produktraum, in dem die zufällige Folge
bezeichnen wir den
Produktraum, in dem die zufällige Folge 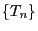 ihre Werte
annimmt,
ihre Werte
annimmt,
- und mit
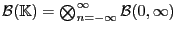 die
die 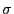 -Algebra der Borel-Mengen in
-Algebra der Borel-Mengen in
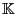 .
.
- Die Verteilung von
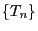 über
über
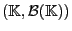 bezeichnen
wir mit
bezeichnen
wir mit 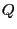 .
.
- Außerdem betrachten wir den Verschiebungsoperator
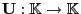 mit
mit
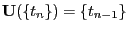 .
.
- Weil
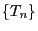 stationär ist, ergibt sich aus (6),
dass die Verteilung
stationär ist, ergibt sich aus (6),
dass die Verteilung 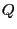 von
von 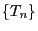 invariant bezüglich
invariant bezüglich
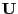 ist, d.h., es gilt
ist, d.h., es gilt
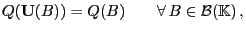 |
(8) |
wobei
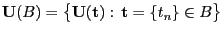 .
.
- Ausgehend von der ,,folgenstationären'' Verteilung
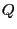 über
über
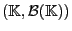 , die die Invarianzeigenschaft
(8) besitzt, kann man nun einen Zählprozess
, die die Invarianzeigenschaft
(8) besitzt, kann man nun einen Zählprozess
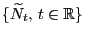 mit stationären Zuwächsen
konstruieren.
mit stationären Zuwächsen
konstruieren.
- Außerdem betrachten wir für jedes
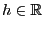 den
(zeitkontinuierlichen) Verschiebungsoperator
den
(zeitkontinuierlichen) Verschiebungsoperator
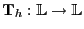
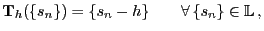 |
(9) |
der
die ,,Punkte'' 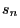 von
von
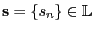 um
um 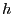 Längeneinheiten nach links bzw. den Ursprung um
Längeneinheiten nach links bzw. den Ursprung um 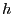 Längeneinheiten nach rechts verschiebt, falls
Längeneinheiten nach rechts verschiebt, falls 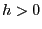 .
.
- Schließlich sei
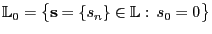 und für jedes
und für jedes
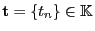 sei die Abbildung
gegeben durch
sei die Abbildung
gegeben durch
- Definition
 Ein Wahrscheinlichkeitsmaß
Ein Wahrscheinlichkeitsmaß 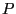 über
über
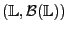 heißt
heißt
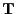 -invariant, wenn
-invariant, wenn
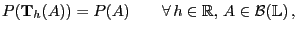 |
(10) |
wobei
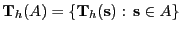 .
.
Theorem 4.4
Sei
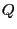
ein
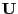
-invariantes Wahrscheinlichkeitsmaß über
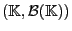
mit
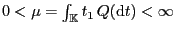
. Dann ist durch den Ansatz
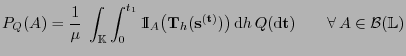 |
(11) |
ein
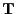
-invariantes Wahrscheinlichkeitsmaß
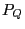
über
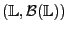
gegeben.
- Beweis
-
- Beachte
 Durch Vertauschung der Integrationsreihenfolge
ergibt sich, dass (11) äquivalent ist mit
Durch Vertauschung der Integrationsreihenfolge
ergibt sich, dass (11) äquivalent ist mit
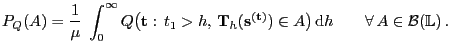 |
(13) |
- Beweis
 Die Behauptung ergibt sich unmittelbar aus der
in Theorem 4.4 gezeigten
Die Behauptung ergibt sich unmittelbar aus der
in Theorem 4.4 gezeigten
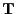 -Invarianz des
Wahrscheinlichkeitsmaßes
-Invarianz des
Wahrscheinlichkeitsmaßes 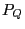 .
.

- Beachte
 Für den in Abschnitt 4.1.1
betrachteten Spezialfall, bei dem die Zwischenankunftszeiten
Für den in Abschnitt 4.1.1
betrachteten Spezialfall, bei dem die Zwischenankunftszeiten
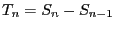 eine Folge von unabhängigen und identisch (exponentiell)
verteilten Zufallsvariablen bilden, kann man sich leicht
überlegen, dass dann der in (14) gegebene
Zählprozess
eine Folge von unabhängigen und identisch (exponentiell)
verteilten Zufallsvariablen bilden, kann man sich leicht
überlegen, dass dann der in (14) gegebene
Zählprozess
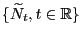 ein homogener
Poisson-Prozess ist.
ein homogener
Poisson-Prozess ist.




Nächste Seite: Erneuerungsprozesse mit stationären Zuwächsen
Aufwärts: Zählprozesse im
Vorherige Seite: Homogener Poisson-Prozess
Inhalt
Jonas Rumpf
2006-07-27
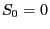 gilt und
gilt und
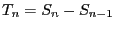 zwischen den
aufeinanderfolgenden Ereigniszeitpunkten
zwischen den
aufeinanderfolgenden Ereigniszeitpunkten 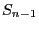 und
und 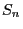 eine beliebige stationäre Folge
eine beliebige stationäre Folge 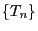 von (nichtnotwendig
unabhängigen) positiven Zufallsvariablen über einem gewissen
Wahrscheinlichkeitsraum
von (nichtnotwendig
unabhängigen) positiven Zufallsvariablen über einem gewissen
Wahrscheinlichkeitsraum
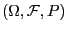 bilden.
bilden.