



Next: Eigenschaften multivariater Verteilungsfunktionen
Up: Zufallsvektoren
Previous: Zufallsvektoren
Contents
Definition, Verteilung und Verteilungsfunktion
Bei Anwendungen besteht oft die Notwendigkeit, nicht nur eine
Kennzahl 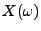 , sondern gleichzeitig mehrere Kennzahlen
, sondern gleichzeitig mehrere Kennzahlen
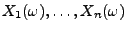 von
von
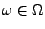 zu
betrachten.
zu
betrachten.
- Beispiele
-
- zweimaliges Würfeln
- Als Grundraum wählen wir so wie bisher
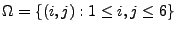 , vgl. Abschnitt 2.4.1.
, vgl. Abschnitt 2.4.1.
- Sei
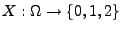 bzw.
bzw.
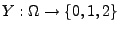 die (zufällige) Anzahl, mit der die Augenzahl ,,6'' bzw. ,,1''
beim zweimaligen Würfeln erzielt wird.
die (zufällige) Anzahl, mit der die Augenzahl ,,6'' bzw. ,,1''
beim zweimaligen Würfeln erzielt wird.
- Dann gilt für
die Wahrscheinlichkeiten
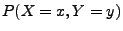 bzw. für
die Einzelwahrscheinlichkeiten
bzw. für
die Einzelwahrscheinlichkeiten 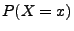 und
und
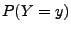 von
von  und
und 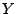 :
:
- Aus der Tabelle kann man auch die Einzelwahrscheinlichkeiten
der Summe
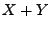 erhalten. Beispielsweise gilt
erhalten. Beispielsweise gilt
- Analog ergibt sich
bzw.
- Analyse von Kommunikationsnetzen
- Betrachten
ein Kommunikationsnetz mit
 Komponenten.
Komponenten.
- Sei
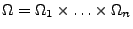 , wobei
, wobei
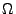 die Menge aller möglichen Momentanzustände
die Menge aller möglichen Momentanzustände
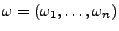 des Netzes und
des Netzes und
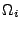 die Menge aller möglichen Momentanzustände
die Menge aller möglichen Momentanzustände 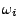 der
der 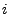 -ten
Komponente bezeichnet;
-ten
Komponente bezeichnet;
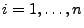 .
.
- Dann kann beispielsweise
durch die Abbildung
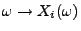 die
Belastung
die
Belastung
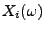 der
der 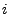 -ten Komponente
in Abhängigkeit vom Momentanzustand
-ten Komponente
in Abhängigkeit vom Momentanzustand 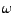 des Netzes
modelliert werden.
des Netzes
modelliert werden.
- Die (globale) Belastung des gesamten Netzes kann
dann durch den Vektor
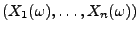 beschrieben werden.
beschrieben werden.
Die gleichzeitige Betrachtung mehrerer Kennzahlen
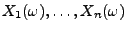 von
von
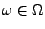 führt zum
Begriff des Zufallsvektors.
führt zum
Begriff des Zufallsvektors.
- Definition
 Sei
Sei
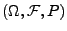 ein beliebiger
Wahrscheinlichkeitsraum, und sei
ein beliebiger
Wahrscheinlichkeitsraum, und sei
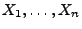 eine
beliebige Folge von Zufallsvariablen
eine
beliebige Folge von Zufallsvariablen
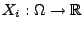 ;
;
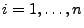 .
.
Theorem 3.7
Die Abbildung
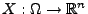
ist genau dann ein Zufallsvektor, wenn
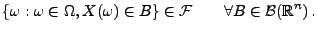 |
(22) |
Die Verteilung
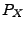
von

wird eindeutig durch die Verteilungsfunktion
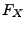
von

bestimmt.
Der Beweis ist analog zum Beweis der
Theoreme 3.1 und 3.4. Er wird deshalb
weggelassen.




Next: Eigenschaften multivariater Verteilungsfunktionen
Up: Zufallsvektoren
Previous: Zufallsvektoren
Contents
Ursa Pantle
2004-05-10
![]() , sondern gleichzeitig mehrere Kennzahlen
, sondern gleichzeitig mehrere Kennzahlen
![]() von
von
![]() zu
betrachten.
zu
betrachten.
![]() von
von
![]() führt zum
Begriff des Zufallsvektors.
führt zum
Begriff des Zufallsvektors.