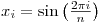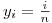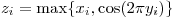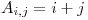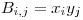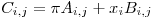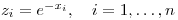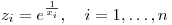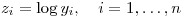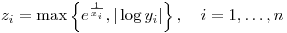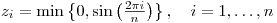Component-wise Arithmetic Operations on Matrices and Vectors
In the following we show some examples for coding component-wise operations on matrices and vectors. The notation that FLENS provides for coding such operations closely follows the typical mathematical notation:
Simply write down the operation component-wise!
The examples will briefly cover the following topics:
- Initialize matrices and vectors component-wise:
- Perform some mathematical operations (e.g. sin, cos,... basically all the stuff from cmath) component-wise
- Simple component-wise summation
- Define your own component-wise mathematical operation
- List of supported mathematical component-wise operations in FLENS
Initialize matrices and vectors component-wise
In this example we will deal with
- vectors
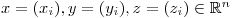 and
and
- matrices
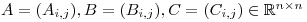 .
.
The matrices and vectors will be initialized as follows:
As you can see, this can be coded close to the mathematical notation in an expressive way:
#include <flens/flens.h>
using namespace flens;
using namespace std;
typedef GeMatrix<FullStorage<double, ColMajor> > DGeMatrix;
typedef DenseVector<Array<double> > DDenseVector;
int
main()
{
int n = 8;
Index i,j;
DDenseVector x(n), y(n), z(n);
DGeMatrix A(n,n), B(n,n), C(n,n);
x(i) = sin(2*M_PI*i/n);
y(i) = i/double(n);
z(i) = max(x(i), cos(2*M_PI*y(i)));
A(i,j) = i + j;
B(i,j) = x(i)*y(j);
C(i,j) = M_PI*A(i,j) + x(i)*B(i,j);
cout << "x = " << x << endl;
cout << "y = " << y << endl;
cout << "z = " << z << endl;
cout << "A = " << A << endl;
cout << "B = " << B << endl;
cout << "C = " << C << endl;
}
This will produce the following result:
x = [ 0.707107 1.000000 0.707107 0.000000 -0.707107 -1.000000 -0.707107 -0.000000 ] y = [ 0.125000 0.250000 0.375000 0.500000 0.625000 0.750000 0.875000 1.000000 ] z = [ 0.707107 1.000000 0.707107 0.000000 -0.707107 -0.000000 0.707107 1.000000 ] A = [8, 8] 2.000000 3.000000 4.000000 5.000000 6.000000 7.000000 8.000000 9.000000 ; 3.000000 4.000000 5.000000 6.000000 7.000000 8.000000 9.000000 10.000000 ; 4.000000 5.000000 6.000000 7.000000 8.000000 9.000000 10.000000 11.000000 ; 5.000000 6.000000 7.000000 8.000000 9.000000 10.000000 11.000000 12.000000 ; 6.000000 7.000000 8.000000 9.000000 10.000000 11.000000 12.000000 13.000000 ; 7.000000 8.000000 9.000000 10.000000 11.000000 12.000000 13.000000 14.000000 ; 8.000000 9.000000 10.000000 11.000000 12.000000 13.000000 14.000000 15.000000 ; 9.000000 10.000000 11.000000 12.000000 13.000000 14.000000 15.000000 16.000000 ; B = [8, 8] 0.088388 0.176777 0.265165 0.353553 0.441942 0.530330 0.618718 0.707107 ; 0.125000 0.250000 0.375000 0.500000 0.625000 0.750000 0.875000 1.000000 ; 0.088388 0.176777 0.265165 0.353553 0.441942 0.530330 0.618718 0.707107 ; 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 ; -0.088388 -0.176777 -0.265165 -0.353553 -0.441942 -0.530330 -0.618718 -0.707107 ; -0.125000 -0.250000 -0.375000 -0.500000 -0.625000 -0.750000 -0.875000 -1.000000 ; -0.088388 -0.176777 -0.265165 -0.353553 -0.441942 -0.530330 -0.618718 -0.707107 ; -0.000000 -0.000000 -0.000000 -0.000000 -0.000000 -0.000000 -0.000000 -0.000000 ; C = [8, 8] 6.345685 9.549778 12.753871 15.957963 19.162056 22.366149 25.570241 28.774334 ; 9.549778 12.816371 16.082963 19.349556 22.616149 25.882741 29.149334 32.415927 ; 12.628871 15.832963 19.037056 22.241149 25.445241 28.649334 31.853427 35.057519 ; 15.707963 18.849556 21.991149 25.132741 28.274334 31.415927 34.557519 37.699112 ; 18.912056 22.116149 25.320241 28.524334 31.728427 34.932519 38.136612 41.340704 ; 22.116149 25.382741 28.649334 31.915927 35.182519 38.449112 41.715704 44.982297 ; 25.195241 28.399334 31.603427 34.807519 38.011612 41.215704 44.419797 47.623890 ; 28.274334 31.415927 34.557519 37.699112 40.840704 43.982297 47.123890 50.265482 ;
Perform some mathematical operations component-wise
In this example we will deal with vectors
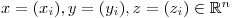
We initialize vectors 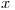 and
and 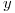 component-wise with
component-wise with
 and
and 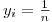 . This is followed by the component-wise
computation of
. This is followed by the component-wise
computation of
Again the code realizing this should be pretty much self-explanatory ...
#include <flens/flens.h>
using namespace flens;
using namespace std;
typedef DenseVector<Array<double> > DDenseVector;
int
main()
{
int n = 8;
Index i;
DDenseVector x(n), y(n), z(n);
x(i) = i*i;
y(i) = double(1)/i;
cout << "x = " << x << endl;
cout << "y = " << y << endl;
z(i) = exp(-x(i));
cout << "z = exp(-x)" << endl << " = " << z << endl;
z(i) = exp(1/x(i));
cout << "z = exp(-x)" << endl << " = " << z << endl;
z(i) = log(y(i));
cout << "z = log(y)" << endl << " = " << z << endl;
z(i) = max(exp(1/x(i)), abs(log(y(i))));
cout << "z = max(exp(1/x), abs(log(y)))" << endl << " = " << z << endl;
z(i) = min(0, sin(2*M_PI*i/n));
cout << "z = min(0, sin(2*M_PI*i/n)" << endl << " = " << z << endl;
}
And here the result:
x = [ 1.000000 4.000000 9.000000 16.000000 25.000000 36.000000 49.000000 64.000000 ] y = [ 1.000000 0.500000 0.333333 0.250000 0.200000 0.166667 0.142857 0.125000 ] z = exp(-x) = [ 0.367879 0.018316 0.000123 0.000000 0.000000 0.000000 0.000000 0.000000 ] z = exp(-x) = [ 2.718282 1.284025 1.117519 1.064494 1.040811 1.028167 1.020618 1.015748 ] z = log(y) = [ 0.000000 -0.693147 -1.098612 -1.386294 -1.609438 -1.791759 -1.945910 -2.079442 ] z = max(exp(1/x), abs(log(y))) = [ 2.718282 1.284025 1.117519 1.386294 1.609438 1.791759 1.945910 2.079442 ] z = min(0, sin(2*M_PI*i/n) = [ 0.000000 0.000000 0.000000 0.000000 -0.707107 -1.000000 -0.707107 -0.000000 ]
Simple component-wise summation
In this example we will deal with
- vectors
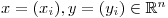 ,
,
- vector
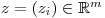 and
and
- matrix
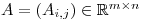 .
.
We will compute:
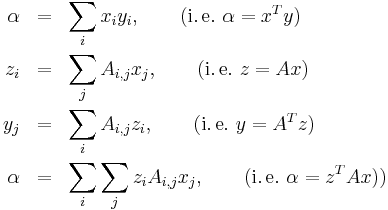
#include <flens/flens.h>
using namespace flens;
using namespace std;
typedef GeMatrix<FullStorage<double, ColMajor> > DGeMatrix;
typedef DenseVector<Array<double> > DDenseVector;
int
main()
{
int m = 4;
int n = 8;
Index i,j;
DDenseVector x(n), y(n);
DDenseVector z(m);
DGeMatrix A(m,n);
// some simple initialization
x(i) = i;
y(i) = n-i;
A(i,j) = n*(i-1) + j;
cout << "x = " << x << endl;
cout << "y = " << y << endl;
cout << "A = " << A << endl;
// ... and here the computations:
double alpha;
// alpha = x^T*y
alpha = sum(x(i)*y(i), i);
cout << "alpha = " << alpha << endl << endl;
// z = A*x
z(i) = sum(A(i,j)*x(j), j);
cout << "z = " << z << endl;
// y = A^T*z
y(j) = sum(A(i,j)*z(i), i);
cout << "y = " << y << endl;
// alpha = z^T A x
alpha = sum(sum(z(i)*A(i,j)*x(j), i), j);
cout << "alpha = " << alpha << endl;
}
And here the result:
x = [ 1.000000 2.000000 3.000000 4.000000 5.000000 6.000000 7.000000 8.000000 ] y = [ 7.000000 6.000000 5.000000 4.000000 3.000000 2.000000 1.000000 0.000000 ] A = [4, 8] 1.000000 2.000000 3.000000 4.000000 5.000000 6.000000 7.000000 8.000000 ; 9.000000 10.000000 11.000000 12.000000 13.000000 14.000000 15.000000 16.000000 ; 17.000000 18.000000 19.000000 20.000000 21.000000 22.000000 23.000000 24.000000 ; 25.000000 26.000000 27.000000 28.000000 29.000000 30.000000 31.000000 32.000000 ; alpha = 84.000000 z = [ 204.000000 492.000000 780.000000 1068.000000 ] y = [ 44592.000000 47136.000000 49680.000000 52224.000000 54768.000000 57312.000000 59856.000000 62400.000000 ] alpha = 2032704.000000
Define your own component-wise mathematical operation
Assume you want to define your own function dummy that can be applied component-wise to a matrix or vector. This is made very simple if your function dummy takes only one or two arguments, i.e. if your function represents an unary or a binary operation respectively.
If your function takes more than two arguments it is still simple but you have to face more of the internals. For the sake of simplicity we will focus here on a simple example where a function dummy takes only one argument, i.e. represents an unary operation.
Assume dummy is defined as follows:
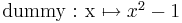
#include <iostream>
#include <flens/flens.h>
namespace flens {
//== 1) define your own operator type ==
struct OpDummy {};
//== 2) define your own function returning a scalar closure ==
template <typename X>
const typename _SUO_<OpDummy, X>::Type
dummy(const ScalarClosure<X> &x)
{
typedef typename _SUO_<OpDummy, X>::Engine SUO;
return SUO(x.engine());
}
//== 3) define how your operation gets evaluated
template <>
struct Operation<OpDummy>
{
template <typename X>
static X
eval(const X &x)
{
return x*x-1; // <- return x^2-1
}
};
} // namespace flens
using namespace flens;
using namespace std;
typedef GeMatrix<FullStorage<double, ColMajor> > DGeMatrix;
typedef DenseVector<Array<double> > DDenseVector;
int
main()
{
DDenseVector x(5), y(5);
Index i;
x(i) = dummy(i);
cout << "x = " << x << endl;
y(i) = dummy(x(i));
cout << "y = " << y << endl;
double alpha = sum(dummy(y(i)), i);
cout << "alpha = " << alpha << endl;
}
And here the result:
x = [ 0.000000 3.000000 8.000000 15.000000 24.000000 ] y = [ -1.000000 8.000000 63.000000 224.000000 575.000000 ] alpha = 384830.000000
Howto: Defining component-wise mathematical operations
First you have to define a new type representing your operation. You do this by defining an empty struct:
struct OpDummy {};
Second you have to implement a function that returns so called scalar closure objects. Such objects encapsulates an operation and allows delaying its evaluation. Don't worry if this scares you. The implementation follows a rather strict pattern. For an unary operation the rough idea is the following: your function receives an object of type
ScalarClosure<X>
where X denotes some template parameter, then creates an object of type
ScalarUnaryOperation<OpDummy, X>
and finally returns an object of type
ScalarClosure<ScalarUnaryOperation<OpDummy, X> >
For convenience we provide a trait class that eases the handling:
_SUO_<OpDummy, X>::Engine for ScalarUnaryOperation<OpDummy, X> _SUO_<OpDummy, X>::Type for ScalarClosure<ScalarUnaryOperation<OpDummy, X> >
We hope that you now have a rough idea what's going on in the code snippet
template <typename X>
const typename _SUO_<OpDummy, X>::Type
dummy(const ScalarClosure<X> &x)
{
typedef typename _SUO_<OpDummy, X>::Engine SUO;
return SUO(x.engine());
}
Finally you have to define how your dummy operation gets carried out. You define this in the Operation trait:
template <>
struct Operation<OpDummy>
{
template <typename X>
static X
eval(const X &x)
{
return x*x-1; // <- return x^2-1
}
};
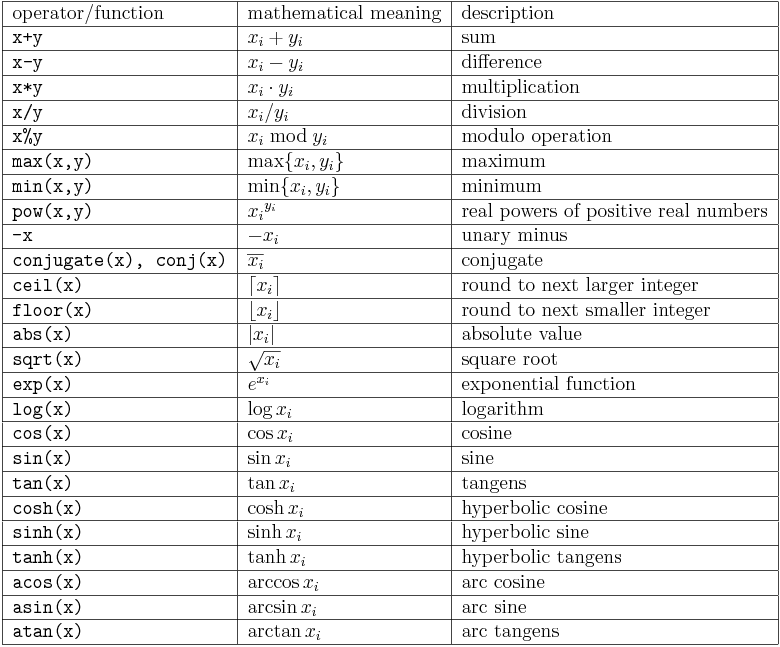
List of supported mathematical component-wise operations in FLENS
So far the following functions/operations are supported in FLENS. The list basically consists of those functions that can be found in cmath (and we therefore use the same names for functions like acos instead of arccos. But maybe we should support both names in such cases). Feel invited to extend this list: