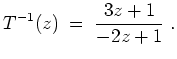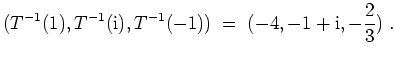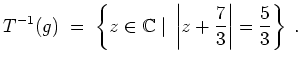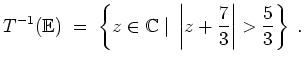- Es sei
Also liegt die Menge
links von
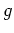 . Die gesuchte Menge
. Die gesuchte Menge
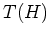 ist also das links von
ist also das links von
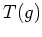 liegende Gebiet.
liegende Gebiet.
Es gilt
Daher ist
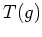 der verallgemeinerte Kreise Gerade mit der Orientierung
der verallgemeinerte Kreise Gerade mit der Orientierung
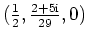 .
Wir wollen
.
Wir wollen
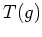 noch genauer bestimmen.
Es sei
Wegen
noch genauer bestimmen.
Es sei
Wegen
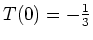 und obigem gilt
und obigem gilt
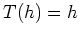 . Ferner schneidet
. Ferner schneidet
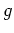 den verallgemeinerten Kreis
den verallgemeinerten Kreis
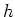 senkrecht in
senkrecht in
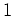 .
Daher schneidet sich
.
Daher schneidet sich
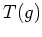 und
und
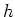 senkrecht in
senkrecht in
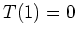 . Somit ist
. Somit ist
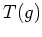 ein Kreis, dessen Mittelpunkt auf der reellen Achse
in der Mitte zwischen
ein Kreis, dessen Mittelpunkt auf der reellen Achse
in der Mitte zwischen
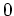 und
und
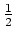 liegt,
d.h. es gilt
Mit der Orientierung von
liegt,
d.h. es gilt
Mit der Orientierung von
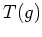 folgt, daß
folgt, daß
- Die Möbiustransformation
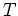 wird durch die Matrix
wird durch die Matrix
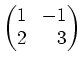 beschrieben, also wird
beschrieben, also wird
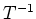 durch die Matrix
durch die Matrix
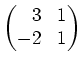 beschrieben. Es folgt also
Die Menge
beschrieben. Es folgt also
Die Menge
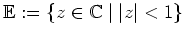 liegt links des verallgemeinerten Kreises
Die gesuchte Menge
liegt links des verallgemeinerten Kreises
Die gesuchte Menge
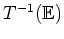 liegt also links des verallgemeinerten Kreises
liegt also links des verallgemeinerten Kreises
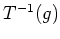 mit der Orientierung
Nun schneiden sich
mit der Orientierung
Nun schneiden sich
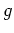 und
und
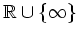 senkrecht in
senkrecht in
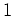 und
und
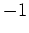 , also schneiden sich
, also schneiden sich
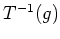 und
und
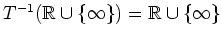 senkrecht in
senkrecht in
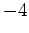 und
und
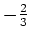 .
Daher ist
.
Daher ist
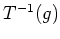 ein Kreis, dessen Mittelpunkt auf der reellen Achse in der Mitte zwischen
ein Kreis, dessen Mittelpunkt auf der reellen Achse in der Mitte zwischen
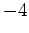 und
und
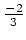 liegt,
d.h. es folgt
Mit der Orientierung von
liegt,
d.h. es folgt
Mit der Orientierung von
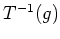 folgt, daß
folgt, daß
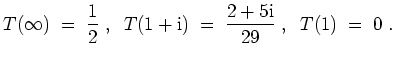
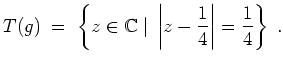
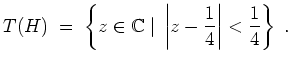
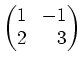 beschrieben, also wird
beschrieben, also wird
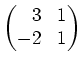 beschrieben. Es folgt also
beschrieben. Es folgt also
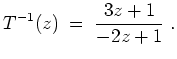
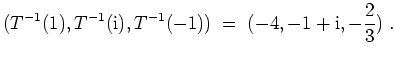
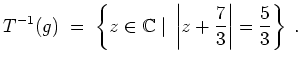
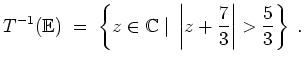
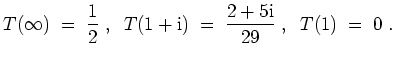
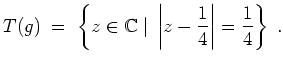
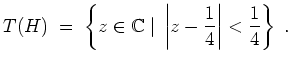
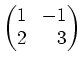 beschrieben, also wird
beschrieben, also wird
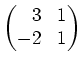 beschrieben. Es folgt also
beschrieben. Es folgt also