Lösung.

  1. Es sei
    $ \mbox{$\displaystyle \gamma:[0,1] \to \mathbb{C}\;,\;\; \gamma(t)\;:=\;(1-t)z_0+tz\;. $}$
    Dann gilt
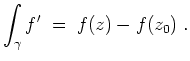
    $ \mbox{$\displaystyle \int_\gamma f' \;=\; f(z)-f(z_0)\;. $}$
    Mit der Standardabschätzung folgt
    $ \mbox{$\displaystyle \begin{array}{rcl} \vert f(z)-f(z_0)\vert &\le& \ell(\g... ...z_0\vert\cdot\sup\{\vert f'(\xi)\vert \;:\; \xi \in [z,z_0] \}\;. \end{array}$}$
  2. (i)
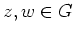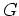    Es seien zunächst $ \mbox{$z,w \in G$}$ derart, daß $ \mbox{$[z,w]$}$ in $ \mbox{$G$}$ enthalten ist. Es folgt
    $ \mbox{$\displaystyle \vert f(z)-f(w)\vert \;\le\;\vert z-w\vert\cdot\sup\{\vert f'(\xi)\vert \;:\; \xi \in [z,w] \}\;=\;0\;. $}$
    Somit gilt
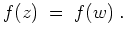
    $ \mbox{$\displaystyle f(z)\;=\;f(w)\;. $}$
    (ii)
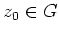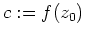    Es sei $ \mbox{$z_0 \in G$}$ und $ \mbox{$c:=f(z_0)$}$ . Wir zeigen, daß die Menge
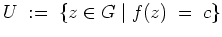
    $ \mbox{$\displaystyle U\;:=\;\{ z \in G \;\vert\; f(z)\;=\;c \} $}$
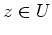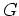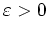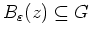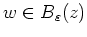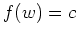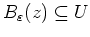    offen ist. Es sei dazu $ \mbox{$z \in U$}$ . Da $ \mbox{$G$}$ offen ist, gibt es ein $ \mbox{$\varepsilon>0$}$ , so daß $ \mbox{$B_\varepsilon(z) \subseteq G$}$ . Dann gilt für alle $ \mbox{$w \in B_\varepsilon(z)$}$ , daß $ \mbox{$[z,w] \subseteq G$}$ , und nach (i) folgt nun $ \mbox{$f(w)=c$}$ . Wir haben damit gezeigt, daß $ \mbox{$B_\varepsilon(z) \subseteq U$}$ . Somit ist $ \mbox{$U$}$ offen.

    Andererseits ist auch die Menge

    $ \mbox{$\displaystyle G\setminus U \;=\; \{z \in G \;\vert\; f(z)\ne c \} \;=\; f^{-1}(\mathbb{C}\setminus\{c\}) $}$
    offen, als stetiges Urbild einer offenen Menge.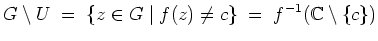

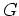    Nun ist $ \mbox{$G$}$ zusammenhängend und es gilt

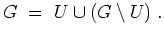
    $ \mbox{$\displaystyle G\;=\; U \cup (G \setminus U)\;. $}$
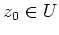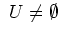    Wegen $ \mbox{$z_0 \in U$}$ ist $ \mbox{$\ U \ne \emptyset$}$ . Daher ist 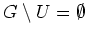$ \mbox{$G \setminus U = \emptyset$}$ , d.h. es gilt 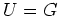$ \mbox{$U=G$}$ und die Behauptung folgt.
    Alternativ zu (ii) hätte man auch wie folgt argumentieren können. Es seien $ \mbox{$z,w \in G$}$ . Da $ \mbox{$G$}$ ein Gebiet ist, lassen sich $ \mbox{$z$}$ und $ \mbox{$w$}$ durch einen Polygonzug in $ \mbox{$G$}$ verbinden. Es gibt also $ \mbox{$z=z_0,z_1, \ldots ,z_n=w \in G$}$ derart, daß $ \mbox{$[z_k,z_{k+1}]\subseteq G$}$ für $ \mbox{$k=0,\ldots,n-1$}$ . Nach (i) gilt $ \mbox{$f(z_k)=f(z_{k+1})$}$ und mit Induktion folgt $ \mbox{$f(z)=f(w)$}$ .