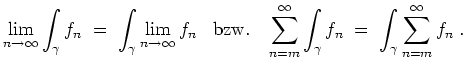Das Riemannintegral einer komplexwertigen Funktion.
Eine Funktion
![]() heißt Riemann-integrierbar, falls die Funktionen
heißt Riemann-integrierbar, falls die Funktionen
![]() und
und
![]() Riemann-integrierbar sind. In diesem Falle heißt
Riemann-integrierbar sind. In diesem Falle heißt
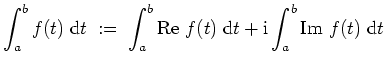
Definition.
Es sei
![]() gegeben. Unter einer Kurve in
gegeben. Unter einer Kurve in
![]() verstehen wir eine stetige Abbildung
verstehen wir eine stetige Abbildung
![]() ,
wobei
,
wobei
![]() ein kompaktes Intervall sei.
Der Träger von
ein kompaktes Intervall sei.
Der Träger von
![]() ist definiert durch
ist definiert durch
Die Kurve
![]() heißt Weg, falls es eine Unterteilung
heißt Weg, falls es eine Unterteilung
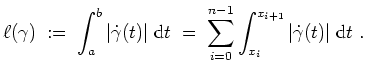
Es sei nun
![]() ein Weg und
ein Weg und
![]() eine stetige Funktion. Dann definieren wir das
Kurvenintegral von
eine stetige Funktion. Dann definieren wir das
Kurvenintegral von
![]() längs
längs
![]() durch
durch
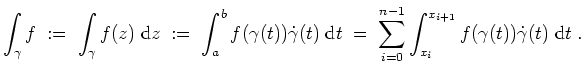
Regeln.
Es seien
![]() ,
,
![]() ein Weg in
ein Weg in
![]() und
und
![]() eine stetige Funktion. Dann gelten folgende Regeln.
eine stetige Funktion. Dann gelten folgende Regeln.
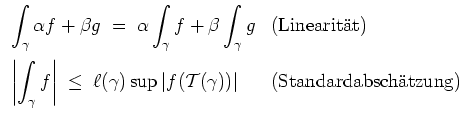
Es sei
![]() eine offene Menge.
Es sei
eine offene Menge.
Es sei
![]() eine Stammfunktion von
eine Stammfunktion von
![]() , d.h. es gelte
, d.h. es gelte
![]() , und
, und
![]() sei ein Weg.
Dann gilt das Analogon zum Hauptsatz der Differential-und Integralrechnung
sei ein Weg.
Dann gilt das Analogon zum Hauptsatz der Differential-und Integralrechnung
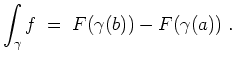
Holomorphie von Kurvenintegralen.
Es seien
![]() eine offene Menge und
eine offene Menge und
![]() ein Weg. Es sei
ein Weg. Es sei
![]() eine Funktion. Für jedes feste
eine Funktion. Für jedes feste
![]() sei die Funktion
sei die Funktion
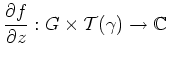
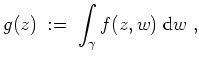
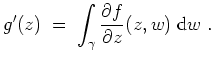
Vertauschung von Grenzwert und Kurvenintegral.
Es sei
![]() ein Weg. Es sei
ein Weg. Es sei
![]() eine Folge von stetigen Funktionen
eine Folge von stetigen Funktionen
![]() so, daß
die Folge
so, daß
die Folge
![]() bzw. die Reihe
bzw. die Reihe
![]() gleichmäßig konvergent auf
gleichmäßig konvergent auf
![]() sei.
Dann gilt
sei.
Dann gilt