Wir definieren
Wir wollen zeigen, daß
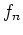 und
und
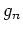 kompakt auf
kompakt auf
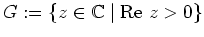 konvergieren.
Dazu sei
konvergieren.
Dazu sei
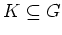 kompakt.
Es sei
kompakt.
Es sei
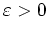 .
Es sei
Dann gilt für
.
Es sei
Dann gilt für
![$ \mbox{$t \in (0,1]$}$](img8.png) und
und
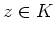 und das Integral
Also konvergiert auch
Wählt man
und das Integral
Also konvergiert auch
Wählt man
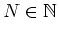 so, daß
für alle
so, daß
für alle
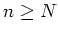 , so folgt
für alle
, so folgt
für alle
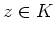 und alle
und alle
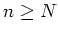 .
Also konvergiert
.
Also konvergiert
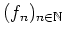 kompakt auf
kompakt auf
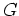 gegen
gegen
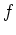 .
.
Es sei
Dann gilt für
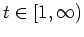 und
und
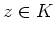 für eine Konstante
für eine Konstante
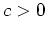 , und das Integral
Also konvergiert auch
Wählt man
, und das Integral
Also konvergiert auch
Wählt man
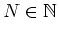 so, daß
für alle
so, daß
für alle
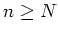 , so folgt
für alle
, so folgt
für alle
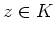 und alle
und alle
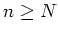 .
Also konvergiert
.
Also konvergiert
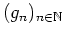 kompakt auf
kompakt auf
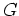 gegen
gegen
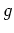 .
.
Nach dem Satz über die Holomorphie von Kurvenintegralen sind
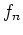 und
und
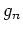 holomorph mit
holomorph mit
Daher ist auch die Summe der beiden Grenzfunktionen
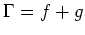 holomorph auf
holomorph auf
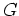 mit
mit
Bemerkung: Wir haben sogar gezeigt, daß die Folge
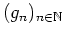 kompakt auf
kompakt auf
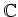 konvergiert, d.h. die Funktion
konvergiert, d.h. die Funktion
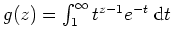 ist eine ganze Funktion.
ist eine ganze Funktion.
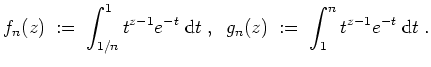
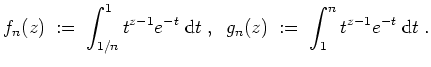
![$ \mbox{$\displaystyle
\int_0^1 t^{\sigma_0-1}\;\text{d}t\;=\; \left[ \frac{t^{\sigma_0}}{\sigma_0}\right]_0^1\;=\;\frac{1}{\sigma_0}\;.
$}$](img11.png)
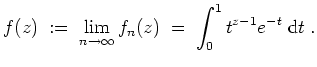
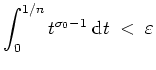
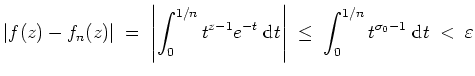
![$ \mbox{$\displaystyle
\int_1^\infty e^{-t/2}\;\text{d}t\;=\; \left[ -\frac{t^{e^{-t/2}}}{2}\right]_1^\infty\;=\;\frac{e^{-1/2}}{2}\;.
$}$](img24.png)
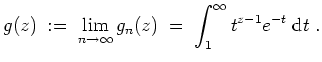
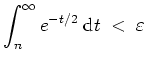
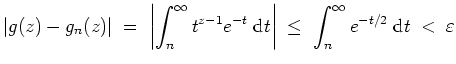
![]() und
und
![]() holomorph mit
holomorph mit
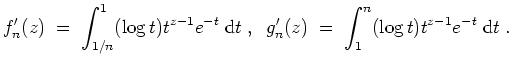
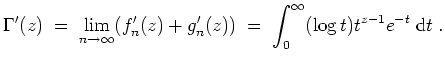
![]() kompakt auf
kompakt auf
![]() konvergiert, d.h. die Funktion
konvergiert, d.h. die Funktion
![]() ist eine ganze Funktion.
ist eine ganze Funktion.