Es seien
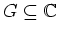 ein Gebiet,
ein Gebiet,
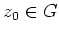 und
und
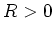 derart, daß
derart, daß
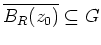 .
Es sei ferner
.
Es sei ferner
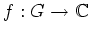 eine holomorphe Funktion. Zeigen Sie.
eine holomorphe Funktion. Zeigen Sie.
-
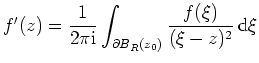 , für alle
, für alle
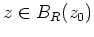 .
.
-
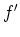 ist holomorph auf
ist holomorph auf
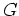 .
.
- Es seien nun
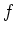 eine ganze Funktion,
eine ganze Funktion,
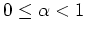 ,
,
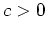 ,
,
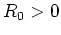 ,
und die Funktion
,
und die Funktion
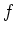 erfülle die Ungleichung
erfülle die Ungleichung
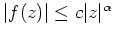 für alle
für alle
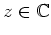 mit
mit
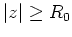 .
Zeigen Sie, daß
.
Zeigen Sie, daß
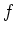 konstant ist.
konstant ist.
![]() ein Gebiet,
ein Gebiet,
![]() und
und
![]() derart, daß
derart, daß
![]() .
Es sei ferner
.
Es sei ferner
![]() eine holomorphe Funktion. Zeigen Sie.
eine holomorphe Funktion. Zeigen Sie.
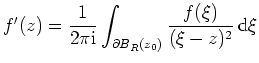 , für alle
, für alle