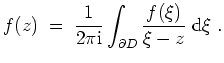Einfacher Zusammenhang.
Ein Gebiet
![]() heißt einfach zusammenhängend, falls sein Komplement
heißt einfach zusammenhängend, falls sein Komplement
![]() zusammenhängend ist.
zusammenhängend ist.
Dafür ist es weder notwendig, noch hinreichend, daß
![]() zusammenhängend ist.
Die geforderte Eigenschaft kann dadurch charakterisiert werden, daß
zusammenhängend ist.
Die geforderte Eigenschaft kann dadurch charakterisiert werden, daß
![]() sich als Vereinigung
zusammenhängender unbeschränkter Mengen schreiben läßt.
sich als Vereinigung
zusammenhängender unbeschränkter Mengen schreiben läßt.
Zum Beispiel ist die geschlitzte Ebene
![]() einfach zusammenhängend.
einfach zusammenhängend.
![\includegraphics[width=8cm]{geschlitzt.eps}](img5.png)
Sternförmige Gebiete sind stets einfach zusammenhängend.
Hingegen ist das Gebiet
![]() nicht einfach zusammenhängend.
Anschaulich bedeutet einfach zusammenhängend, daß das Gebiet
nicht einfach zusammenhängend.
Anschaulich bedeutet einfach zusammenhängend, daß das Gebiet
![]() keine Löcher hat.
keine Löcher hat.
Cauchyscher Integralsatz.
Es seien
![]() ein einfach zusammenhängendes Gebiet,
ein einfach zusammenhängendes Gebiet,
![]() eine holomorphe
Funktion und
eine holomorphe
Funktion und
![]() ein geschlossener Weg in
ein geschlossener Weg in
![]() .
Dann gilt der Cauchysche Integralsatz
.
Dann gilt der Cauchysche Integralsatz
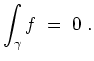
Gleichbedeutend damit ist die Tatsache, daß eine holomorphe Funktion auf einem einfach zusammenhängenden Gebiet stets eine Stammfunktion besitzt.
Cauchysche Integralformel für Kreisscheiben.
Es sei
![]() holomorph und
holomorph und
![]() sei eine offene Kreisscheibe mit
sei eine offene Kreisscheibe mit
![]() .
ist. Es sei
.
ist. Es sei
![]() der positiv orientierte Rand von
der positiv orientierte Rand von
![]() , d.h.
, d.h.
![]() für
für
![]() .
Dann gilt für alle
.
Dann gilt für alle
![]() die Cauchysche Integralformel
die Cauchysche Integralformel