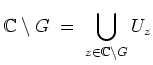Wir wollen zeigen, daß sich
![]() als Vereinigung zusammenhängender unbeschränkter Mengen schreiben läßt.
Es sei etwa
als Vereinigung zusammenhängender unbeschränkter Mengen schreiben läßt.
Es sei etwa
![]() sternförmig bezüglich
sternförmig bezüglich
![]() , und es sei
, und es sei
![]() .
.
Dann gilt
Skizze.
![\includegraphics[width=8cm]{stern.eps}](img6.png)
Die Tatsache
![]() folgt dabei aus der Sternförmigkeit von
folgt dabei aus der Sternförmigkeit von
![]() . Wäre nämlich
. Wäre nämlich
![]() , etwa
, etwa
![]() für ein
für ein
![]() , so wäre auch
, so wäre auch
![]() , im Widerspruch zu
, im Widerspruch zu
![]() .
.
Also haben wir
![]() als Vereinigung zusammenhängender unbeschränkter Mengen
als Vereinigung zusammenhängender unbeschränkter Mengen