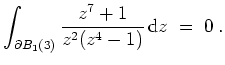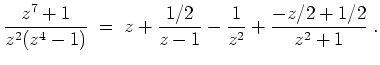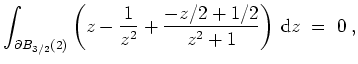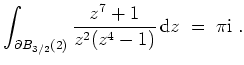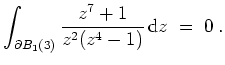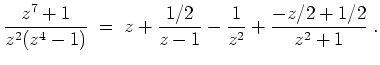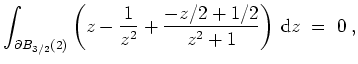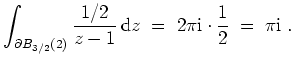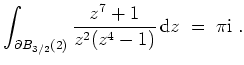- Die Funktion
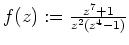 ist holomorph auf
ist holomorph auf
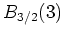 , denn die Nullstellen
des Nenners liegen außerhalb von
, denn die Nullstellen
des Nenners liegen außerhalb von
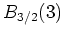 .
Mit dem Cauchyschen Integralsatz folgt
.
Mit dem Cauchyschen Integralsatz folgt
- Mit Partialbruchzerlegung ergibt sich
Wendet man den Cauchyschen Integralsatz auf das Gebiet
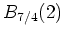 an, so ergibt sich
denn die betrachtete Funktion ist auf
an, so ergibt sich
denn die betrachtete Funktion ist auf
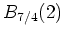 holomorph.
Mit der Cauchyschen Integralformel wird
Insgesamt ergibt sich also
holomorph.
Mit der Cauchyschen Integralformel wird
Insgesamt ergibt sich also