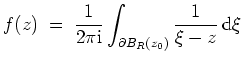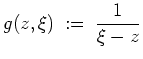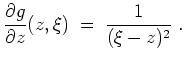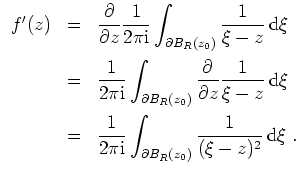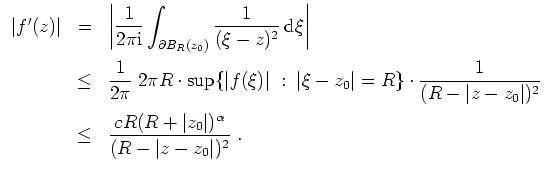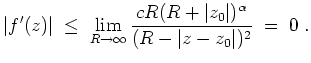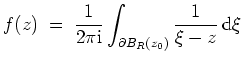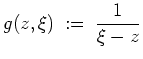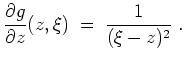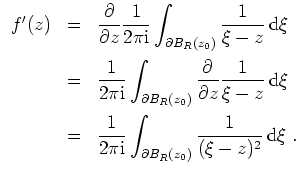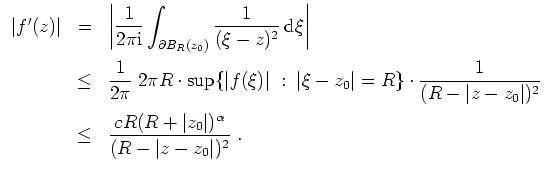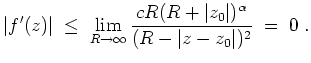- Die Cauchysche Integralformel besagt, daß
gilt für alle
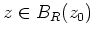 . Nun ist der Integrand
als Funktion zweier Veränderlicher stetig auf
. Nun ist der Integrand
als Funktion zweier Veränderlicher stetig auf
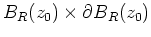 und holomorph als Funktion von
und holomorph als Funktion von
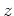 mit
Damit ist auch
mit
Damit ist auch
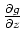 als Funktion zweier Veränderlicher stetig auf
als Funktion zweier Veränderlicher stetig auf
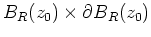 .
Also sind die Voraussetzungen des Satzes über die Holomorphie von Parameterintegralen erfüllt, und es folgt
.
Also sind die Voraussetzungen des Satzes über die Holomorphie von Parameterintegralen erfüllt, und es folgt
- Dieselbe Argumentation kann nun auf den Integranden
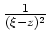 in der obigen Gleichung angewandt werden.
Dieser ist stetig als Funktion zweier Veränderlicher auf
in der obigen Gleichung angewandt werden.
Dieser ist stetig als Funktion zweier Veränderlicher auf
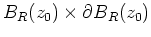 und holomorph als Funktiobn von
und holomorph als Funktiobn von
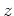 ,
und seine Ableitung nach
,
und seine Ableitung nach
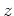 ist
ist
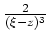 , also ebenfalls stetig auf
, also ebenfalls stetig auf
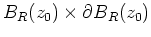 .
Nach dem Satz über die Holomorphie von Parameterintegralen und der Gleichung aus 1. folgt, daß
.
Nach dem Satz über die Holomorphie von Parameterintegralen und der Gleichung aus 1. folgt, daß
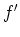 holomorph auf
holomorph auf
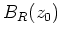 ist.
Da
ist.
Da
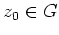 beliebig gewählt werden kann, ist
beliebig gewählt werden kann, ist
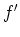 sogar holomorph auf
sogar holomorph auf
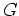 .
.
- Es sei
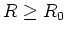 .
Wendet man die Standardabschätzung auf das Integral in 1. an, so ergibt sich mit
.
Wendet man die Standardabschätzung auf das Integral in 1. an, so ergibt sich mit
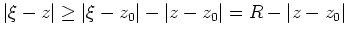 , daß
In dieser Formel kann nun
, daß
In dieser Formel kann nun
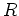 beliebig groß gewählt werden. Also folgt
Daraus folgt
beliebig groß gewählt werden. Also folgt
Daraus folgt
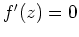 für alle
für alle
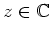 . Daher ist
. Daher ist
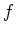 konstant auf
konstant auf
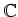 .
.