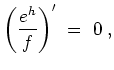Logarithmus holomorpher Funktionen.

Definition.

Es sei ein Gebiet, und sei eine holomorphe Funktion. Unter einem Logarithmus von verstehen wir eine holomorphe Funktion mit .

Bezeichnung: .

Für die Existenz eines Logarithmus von ist es notwendig, daß für alle . Diese Voraussetzung ist jedoch nicht hinreichend, wie das Beispiel , zeigt.

Falls ein Logarithmus von existiert, so ist er bis auf eine additive Konstante der Form , , eindeutig bestimmt. Daher spricht man auch von einem Zweig des Logarithmus von .

Vorsicht: Im allgemeinen ist nicht dasselbe wie die Verkettung von mit dem Hauptzweig der Logarithmusfunktion . Nur falls gilt, so ist ein Logarithmus von .

Eigenschaften.

Es seien und wie oben. Es sei ferner eine stetige Funktion. Dann sind folgende Aussagen äquivalent.

• ist ein Logarithmus von .
• .
• ist holomorph, und es gibt ein mit .

Hinreichendes Kriterium.

Es sei ein einfach zusammenhängendes Gebiet, und sei eine holomorphe Funktion mit für alle . Dann existiert ein Logarithmus von .

Man berechne dazu eine Stammfunktion von ; eine solche existiert, da einfach zusammenhängend ist. Dann folgt