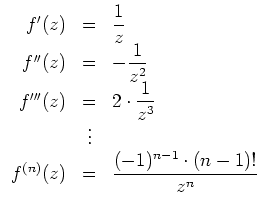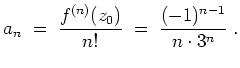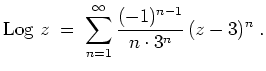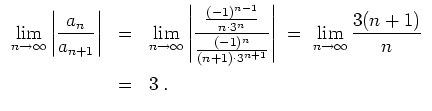Lösung.

Es sei 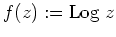$ \mbox{$f(z):=\text{Log }z$}$ . Dann folgt

$ \mbox{$\displaystyle \begin{array}{rclcl} f'(z)&=& \dfrac{1}{z}\\ f''(z)... ...ts& \\ f^{(n)}(z) &=& \dfrac{(-1)^{n-1} \cdot (n-1)!}{z^n} \end{array} $}$
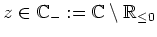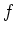für alle $ \mbox{$z\in\mathbb{C}_-:=\mathbb{C}\setminus\mathbb{R}_{\le 0}$}$ . Da $ \mbox{$f$}$ holomorph auf 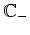$ \mbox{$\mathbb{C}_-$}$ ist, besitzt 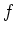$ \mbox{$f$}$ eine Potenzreihenentwicklung um 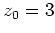$ \mbox{$z_0=3$}$ mit Koeffizienten
$ \mbox{$\displaystyle a_n \;=\; \frac{f^{(n)}(z_0)}{n!} \;=\; \frac{(-1)^{n-1}}{n\cdot 3^n}\;. $}$
Daher ergibt sich die Potenzreihe
$ \mbox{$\displaystyle \textrm{Log }z \;=\; \sum_{n=1}^\infty \frac{(-1)^{n-1}}{n\cdot 3^n}\, (z-3)^n \;. $}$
Der Konvergenzradius dieser Reihe ist
$ \mbox{$\displaystyle \begin{array}{rcl} \displaystyle\lim_{n \to \infty}\le... ...nfty}\dfrac{3(n+1)}{n} \right\vert\vspace*{2mm}\\ &=& 3 \;. \end{array} $}$
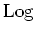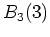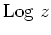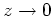Der Konvergenzradius ergibt sich auch aus der Tatsache, daß $ \mbox{$\text{Log}$}$ holomorph auf $ \mbox{$B_3(3)$}$ ist, aber $ \mbox{$\text{Log }z$}$ für $ \mbox{$z\to 0$}$ nicht konvergiert.