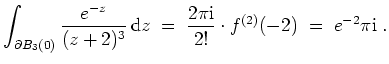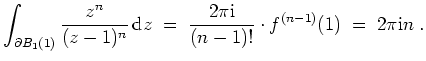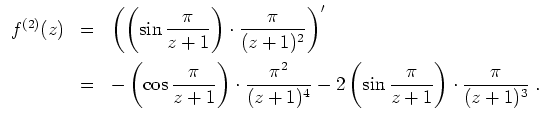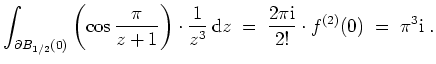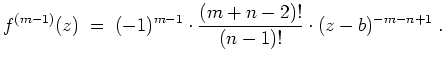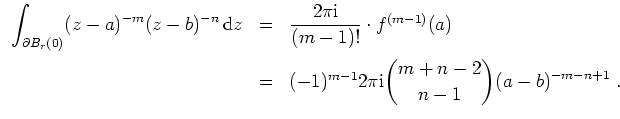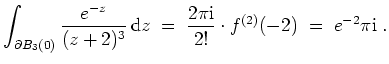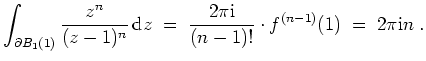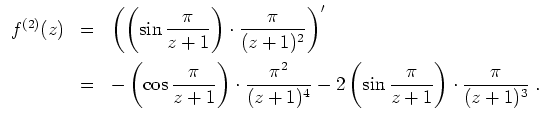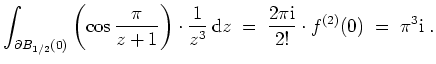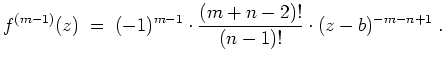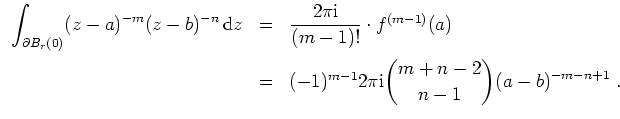- Es sei
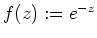 . Nach der Cauchyschen Integralformel für die
. Nach der Cauchyschen Integralformel für die
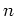 -te Ableitung mit
-te Ableitung mit
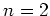 ergibt sich
ergibt sich
- Es sei
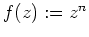 . Nach der Cauchyschen Integralformel für die
. Nach der Cauchyschen Integralformel für die
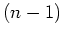 -te Ableitung ergibt sich
-te Ableitung ergibt sich
- Es sei
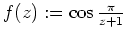 . Dann ist
. Dann ist
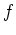 holomorph auf
holomorph auf
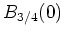 , und es gilt
Nach der Cauchyschen Integralformel für die
, und es gilt
Nach der Cauchyschen Integralformel für die
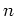 -te Ableitung mit
-te Ableitung mit
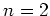 ergibt sich
ergibt sich
- Es sei
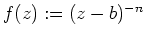 . Dann ist
. Dann ist
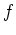 holomorph auf
holomorph auf
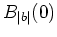 , und es gilt
Nach der Cauchyschen Integralformel für die
, und es gilt
Nach der Cauchyschen Integralformel für die
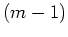 -te Ableitung ergibt sich
-te Ableitung ergibt sich