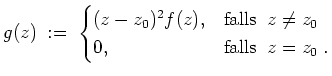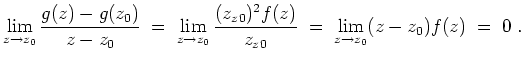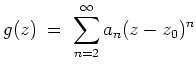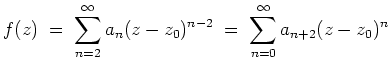Es sei
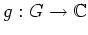 definiert durch
definiert durch
Dann ist
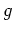 holomorph auf
holomorph auf
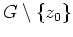 . Andererseits gilt
Daher ist
. Andererseits gilt
Daher ist
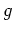 auch differenzierbar im Punkt
auch differenzierbar im Punkt
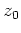 mit
Also besitzt
mit
Also besitzt
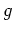 eine Potenzreihenentwicklung der Form
für alle
eine Potenzreihenentwicklung der Form
für alle
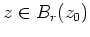 , für ein
, für ein
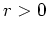 . Daraus folgt
für alle
. Daraus folgt
für alle
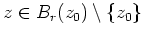 , und diese Potenzreihendarstellung zeigt, daß
, und diese Potenzreihendarstellung zeigt, daß
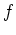 holomorph auf ganz
holomorph auf ganz
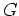 fortgesetzt werden kann,
indem man
setzt.
fortgesetzt werden kann,
indem man
setzt.
![]() definiert durch
definiert durch