Potenzreihenentwicklung und der Satz von Liouville.

Potenzreihenentwicklung holomorpher Funktionen.

Es seien $ \mbox{$G\subseteq\mathbb{C}$}$ ein Gebiet, $ \mbox{$z_0\in G$}$ und $ \mbox{$f:G\to\mathbb{C}$}$ sei eine holomorphe Funktion. Es sei $ \mbox{$r>0$}$ derart, daß $ \mbox{$B_r(z_0)\subseteq G$}$ . Dann läßt sich $ \mbox{$f$}$ als Potenzreihe um $ \mbox{$z_0$}$ entwickeln in der Form

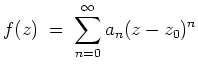
$ \mbox{$\displaystyle f(z) \;=\; \sum_{n=0}^\infty a_n (z-z_0)^n $}$
für alle $ \mbox{$z\in B_r(z_0)$}$ mit eindeutig bestimmten Koeffizienten $ \mbox{$a_n\in\mathbb{C}$}$ . Insbesondere ist $ \mbox{$f$}$ auf $ \mbox{$G$}$ unendlich oft komplex differenzierbar.

Für den Konvergenzradius $ \mbox{$R$}$ der Potenzreihe gilt

$ \mbox{$\displaystyle R \;\ge\; \inf\{\vert z-z_0\vert\;:\; z\in\mathbb{C}\setminus G\} \;=:\; d(z_0,\mathbb{C}\setminus G)\;, $}$
d.h. $ \mbox{$R$}$ ist mindestens so groß wie der Radius der größten Kreisscheibe um $ \mbox{$z_0$}$ , die noch in $ \mbox{$G$}$ enthalten ist. Insbesondere gilt $ \mbox{$R\ge r$}$ .

Skizze.

\includegraphics[width=8cm]{radius.eps}

Für die Koeffizienten $ \mbox{$a_n$}$ gilt

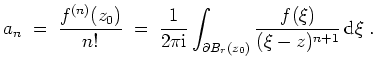
$ \mbox{$\displaystyle a_n \;=\; \dfrac{f^{(n)}(z_0)}{n!} \;=\; \dfrac{1}{2\pi\text{i}}\int_{\partial B_r(z_0)}\dfrac{f(\xi)}{(\xi-z)^{n+1}}\,\text{d}\xi\;. $}$
Dabei ist zusätzlich $ \mbox{$\overline{B_r(z_0)}\subseteq G$}$ vorausgesetzt, d.h. $ \mbox{$0<r<R$}$ . Durch Umstellen dieser Formel ergibt sich die Cauchysche Integralformel für die $ \mbox{$n$}$ -te Ableitung
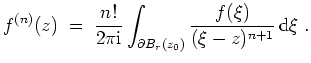
$ \mbox{$\displaystyle f^{(n)}(z) \;=\; \dfrac{n!}{2\pi\text{i}}\int_{\partial B_r(z_0)}\dfrac{f(\xi)}{(\xi-z)^{n+1}}\,\text{d}\xi\;. $}$

Der Satz von Liouville.

Es sei $ \mbox{$f$}$ eine ganze beschränkte Funktion $ \mbox{$\mathbb{C}\to\mathbb{C}$}$ . Dann besagt der Satz von Liouville, daß $ \mbox{$f$}$ konstant ist.